Four Points on a Semicircle
A semicircle has A B as the endpoints of its diameter, and A B = 4 0 0 . Points C and D are on the circumference of the semicircle such that A D = B C = 1 0 0 . What is the length of D C ?
Details and assumptions:
- Lengths given are always the straight line distance between two points, unless otherwise indicated.
The answer is 350.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
aswome solution and the most easiest .....
Let the centre of the circle be point E . By the Law of Cosines, the angle ∠ A E D = arccos 2 ( 2 0 0 ) ( 2 0 0 ) 2 0 0 2 + 2 0 0 2 − 1 0 0 2 = arccos 8 7 . Thus, ∠ D E C = 1 8 0 − 2 arccos 8 7 . Applying the Law of Cosines one more time yields D C = 2 0 0 2 + 2 0 0 2 − 2 ( 2 0 0 ) ( 2 0 0 ) cos ( 1 8 0 − 2 arccos 8 7 ) = 3 5 0 .
In this question, we have a cyclic quadrilateral. According to Ptolemy's theorem, sum of, product of, lengths of opposite sides is equal to product of lengths of diagonals of the cyclic quadrilateral. Here, we have, AC \times BD = AB \times DC + AD \times BC .......(1) When we draw the diagonals we get two right angled triangles, namely triangle ADB (right angled at D since, angle in a semi-circle is a right angle). and triangle ACB right angled at C. By Pythagoras theorem we have value of diagonals as \sqrt{400^2 - 100^2} which will be \sqrt{150000} . Hence product of diagonals = 150000. On substituting in (1) we have 150000 = 400 DC +100 100 i.e., 140000 = 400*DC which gives us the value of DC as 350.
Let A C and B D intersect at X . Then let D X = C X = a , and A X = B X = b . Due to the properties of a semicircle, it is clear ∠ A C B = ∠ A D B = 9 0 ∘ , and as such, we may find via Pythagoras' Theorem that: (1) a 2 + 1 0 0 2 = b 2 (2) ( a + b ) 2 + 1 0 0 2 = 4 0 0 2
Solving these two simultanously, we are able to find that b a = 8 7 . Finally, we note that by similar triangles △ A B X and △ C X D , we have that C D a = 4 0 0 b , and hence C D = 4 0 0 ( b a ) . And hence our answer is 3 5 0 .
Ptolemy's Theorem tells us that AB * DC + AD * BC = AC * BD
Since C and D are points on a semicircle with diameter AB , triangles ACB and ADB are right; they're also congruent, with AC = BD = sqrt{400^2 - 100^2} = sqrt{150000} by Pythagoras.
Then AB * DC + AD * BC = sqrt{150000}^2, and by plugging in known values, we get that 400 * DC = 150000 - 10000 = 140000, or that DC = 350.
Let O be the centre of the semicircle. Now join O D & O C . Now draw a perpendicular from E D on A O and C F on O B . [He likely means "drop a perpendicular from D to A O intersecting at E ". - Calvin] Now in Right angled triangle O E D , we have ( O E ) 2 + ( E D ) 2 = ( O D ) 2 ( O D =radius of the circle=200). Similarly in Right angled triangle A E D , ( A E ) 2 + ( E D ) 2 = ( A D ) 2 (given AD=100).
Thus ( 2 0 0 − O E ) 2 + ( E D ) 2 = ( 1 0 0 ) 2 ( E D ) 2 = ( 1 0 0 ) 2 − ( 2 0 0 − O E ) 2 . Now putting the value of ( E D ) 2 in the equation of triangle O E D , we get, ( 1 0 0 ) 2 − ( 2 0 0 − O E ) 2 + ( O E ) 2 = ( 4 0 0 ) 2 . By solving this we get O E = 1 7 5 . Now in triangle in A O D & B O C , since O A = B O , ∠ A O D = ∠ B O C and O D = O C , so triangle A O D & B O C are congruent by SAS(side-angle-side) congruency. so O E = O F and hence 2 ( O E ) = E F = 3 5 0 . Now E F = D C = 3 5 0 .
[Latex Edits. Edits for clarity - Calvin]
There are many approaches that would work for this problem, due to the symmetry and presence of right angles.
Remember to explain your notation properly. I am unable to guess which angles are θ 1 and θ 2 , if you do not define them somewhere. Likewise in the first solution, you should not make the reader guess what E and F are due to the ambiguous definition. "Draw a perpendicular from E D on A O " doesn't make sense.
If O is the midpoint of A B , let α be the measure of ∠ A O D .
By bisecting ∠ A O D , observe that
- sin 2 α = 2 A O A D = 4 1
- cos 2 α = 1 − ( 4 1 ) 2 = 4 1 5 .
and so, sin α = 2 sin 2 α cos 2 α = 8 1 5 .
Now let P be the midpoint of D C . Clearly D C is parallel to A B and ∠ A O P is a right angle, so ∠ A O D and ∠ D O P are complimentary. Therefore, if β is the measure of ∠ D O P , we have sin β = cos α = 1 − ( 8 1 5 ) ² = 8 7 .
Finally, D C = 2 D P = 2 O D ⋅ sin β = 3 5 0 .
as ABCD cyclic let DC=x , 100 100+400 x=400^2-100^2, it follows x=350 immidiately.
using properties of cyclic quadrilateral ac+bd=pq where a,b,c,d are side lengths and p,q are length of the two diagonals. Lengths of the two diagonals can be found using pythagoras theorem(angle in a semicircle is right angle).
DC = AC cos(theta1) - AD cos(theta2) = AC (AC/AB) - AD (AD/AB) = (AC^2 - AD^2)/AB = (AB^2 - 2 AD^2)/AB = (400^2 - 2 100^2)/400 = Ans
Solution 1: Since A B is the diameter, we have ∠ A D B = 9 0 ∘ . Drop a perpendicular from D to A B at E . So, we have triangles A E D and A D B are similar by angle-angle-angle. Thus A D A E = A B A D ⇒ A E = 4 0 0 1 0 0 ⋅ 1 0 0 = 2 5 .
Let O be the center of the semicircle. By symmetry, we have D C = 2 ⋅ O E = 2 ⋅ ( O A − E A ) = 2 ⋅ ( 2 0 0 − 2 5 ) = 3 5 0 .
Solution 2: Since A D = B C , so ∠ D B A = ∠ C A B = ∠ C D B , so A B ∥ D C , which makes A B C D an isosceles trapezium.
Let O be the center of the semicircle. Then O A D and O B C are congruent isosceles triangles. Let ∠ D A O = α . Then, ∠ A D O = α , ∠ D O A = 1 8 0 ∘ − 2 α , ∠ O D C = 1 8 0 ∘ − 2 α , ∠ C O B = 1 8 0 ∘ − 2 α , ∠ D O C = 4 α − 1 8 0 ∘ .
By sine rule, sin ( 1 8 0 ∘ − 2 α ) A D = sin α A O ⇒ 4 sin 2 α = sin α ⇒ 4 sin α cos α = sin α . Since α = 0 , so sin α = 0 and thus cos α = 4 1 .
By sine rule, we have sin ( 4 α − 1 8 0 ∘ ) D C = sin ( 1 8 0 ∘ − 2 α ) O C ⇒ D C = sin 2 α 2 0 0 × ( − sin 4 α ) = − 2 0 0 × 2 × cos 2 α = − 4 0 0 ( 2 ( 4 1 ) 2 − 1 ) = − 4 0 0 ( − 8 7 ) = 3 5 0 .
Note: There is another solution by Pythagorean Theorem + Ptolemy's Theorem.
We can solve it by using geometric mean Assume that AB=CD+2x
Because ACB is a right triange .. (BC)^2=x.(AB) 100^2=400x x=25
So
CD=AB-2x=400-2(25)=350
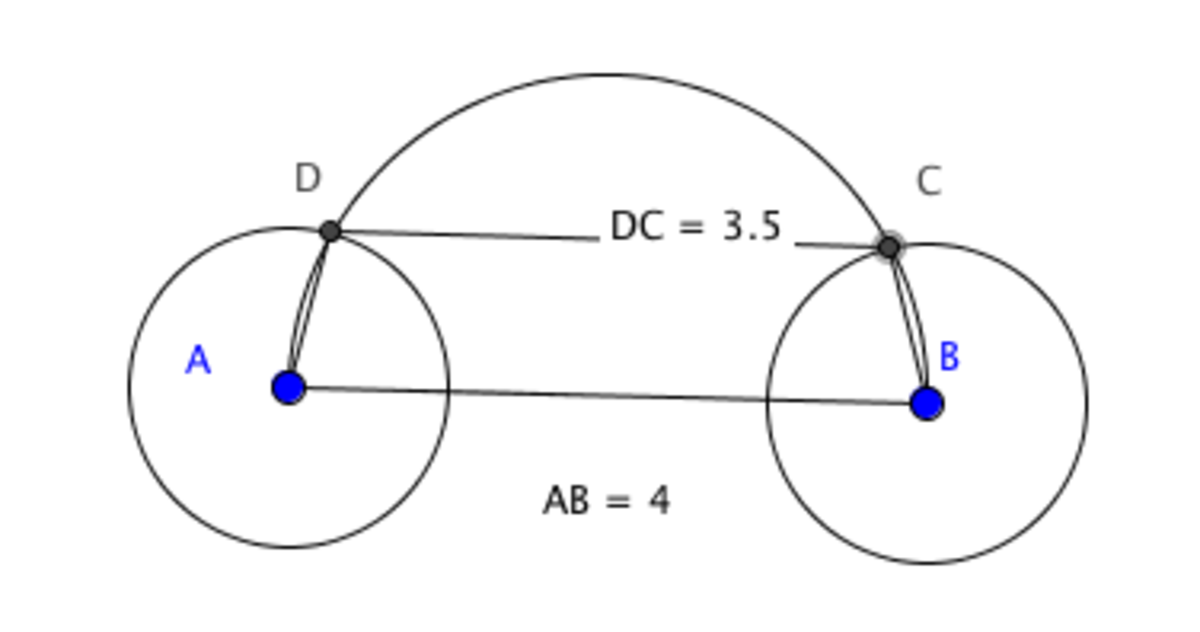
A B subtends a right angle at C (or D ). By pythagoras, A C 2 = A B 2 − B C 2 = 1 6 0 0 0 0 − 1 0 0 0 0 = 1 5 0 0 0 0 , A C = 1 0 0 1 5 = B D . Let D C = x . Now by applying Ptolemy's Theorem to the cyclic quadrilateral A B C D , We have A D ∗ B C + A B ∗ C D = A C ∗ B D so ( 1 0 0 ) ( 1 0 0 ) + ( 4 0 0 ) ( x ) = 1 5 0 0 0 0 . x = 3 5 0 on simplification.
[LaTeX edits - Calvin]