Four Right Triangles in One
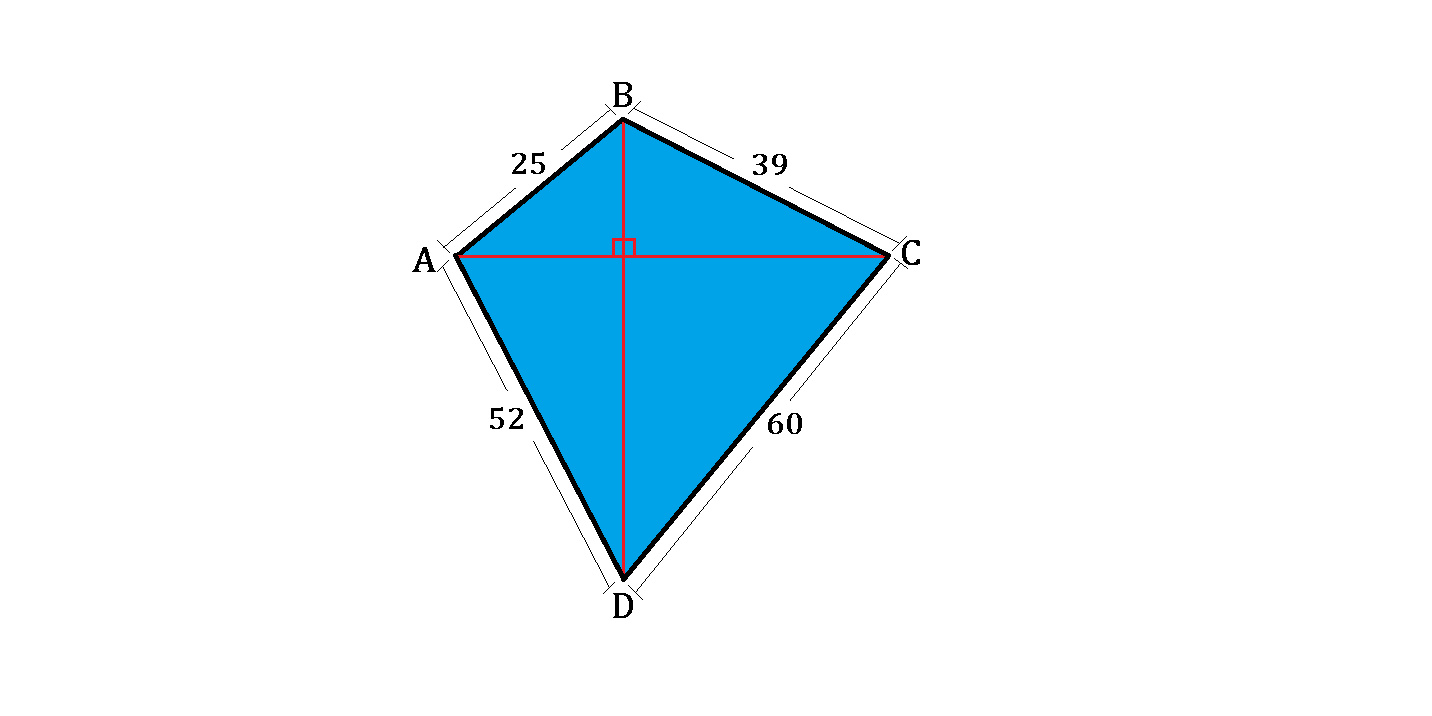
Let A B C D be a quadrilateral with A B = 2 5 , B C = 3 9 , C D = 6 0 , and D A = 5 2 , as shown above.
If the two diagonals are perpendicular to each other, yielding 4 Pythagorean triples for the 4 right triangles, and A C : B D = 8 : 9 , what is the area of quadrilateral A B C D ?
The answer is 1764.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Why is it necessary to get integral diagonals??
The only possible triplets with 2 5 as the hypotenuse are ( 7 , 2 4 , 2 5 ) and ( 1 5 , 2 0 , 2 5 ) . This can be checked using the Euclid's formula of triples.
We need to choose O B , the common side of △ A O B and △ B O C , from the above triples such that O C is an integer.
Now,
3 9 2 − 7 2 = ( 3 9 + 7 ) ( 3 9 − 7 ) = 4 6 × 3 2
3 9 2 − 2 4 2 = ( 3 9 + 2 4 ) ( 3 9 − 2 4 ) = 6 3 × 1 5
3 9 2 − 1 5 2 = ( 3 9 + 1 5 ) ( 3 9 − 1 5 ) = 5 4 × 2 4
3 9 2 − 2 0 2 = ( 3 9 + 2 0 ) ( 3 9 − 2 0 ) = 5 9 × 1 9
Out of these only the third case yields a perfect square.
So, O B = 1 5 units and O C = 3 6
The other sides are:
O A = 2 0 , O D = 4 8 units
∴ Area = 2 D 1 D 2 = 2 5 6 × 6 3 = 1 7 6 4 unit²
Let BE=a and EC=b and AE=c.
a square+b square=39 square.
a square+c square=25 square.
b square-c square=896.
(b-c)(b+c)=896
writing all factors:
1 x 896
2 x 448
4 x 224
7 X 128
8 x 112
14 x 64
16 x 56
28 x 32
b-c < b+c and 2b<78
so only 16 X 56 and 28 X 32 are valid
For 16 x 56,
b-c=16 and b+c=56
2b=72
b=36 and c=20 so a=15 and EB=48
checking 56/63=AC/BD satisfies the condition.
so .5[15x20+15x36+36x48+20x48]=1764.
Relevant wiki: Pythagorean Triples
Suppose the diagonals intersect each other at point E.
And we know that AC : BD = 8 : 9, so suppose AC = 8k and BD = 9k for some constant k.
Suppose AE = x and BE = y. Then we will obtain the system of equations below:
x 2 + y 2 = 2 5 2 _(1)
y 2 + ( 8 k − x ) 2 = 3 9 2 _(2)
( 8 k − x ) 2 + ( 9 k − y ) 2 = 6 0 2 _(3)
( 9 k − y ) 2 + x 2 = 5 2 2 _(4)
Subtracting equation (2) with (1);
( 8 k − x ) 2 − x 2 = 3 9 2 − 2 5 2 = 8 9 6
6 4 k 2 − 1 6 k x = 8 9 6
6 4 k 2 − 8 9 6 = 1 6 k x
x = 4 k − k 5 6
Now subtracting equation (4) with (1);
( 9 k − y ) 2 − y 2 = 5 2 2 − 2 5 2 = 2 0 7 9
8 1 k 2 − 1 8 k y = 2 0 7 9
8 1 k 2 − 2 0 7 9 = 1 8 k y
y = 2 9 k − 2 k 2 3 1
Substituting k terms for x and y in equation (1):
( 4 k − 5 6 / k ) 2 + ( 2 9 k − 2 k 2 3 1 ) 2 = 6 2 5
Multiplying by 4k2 both sides;
( 8 k 2 − 1 1 2 ) 2 + ( 9 k 2 − 2 3 1 ) 2 = 2 5 0 0 k 2
6 4 k 4 − 1 7 9 2 k 2 + 1 2 5 4 4 + 8 1 k 4 − 4 1 5 8 k 2 + 5 3 3 6 1 = 2 5 0 0 k 2
1 4 5 k 4 − 8 4 5 0 k 2 + 6 5 9 0 5 = 0
2 9 k 4 − 1 6 9 0 k 2 + 1 3 1 8 1 = 0
( k 2 − 4 9 ) ( 2 9 k 2 − 2 6 9 ) = 0
Only k = 7 will result in diagonals of integer lengths.
Therefore, x = 4 × 7 − 7 5 6 = 2 0 .
And y = 2 6 3 − 1 4 2 3 1 = 2 6 3 − 3 3 = 1 5 .
Then we will get C E 2 = 3 9 2 − 1 5 2 = 3 6 2 . C E = 3 6 .
Finally, D E 2 = 6 0 2 − 3 6 2 = 4 8 2 . D E = 4 8 .
As a result, A C = 2 0 + 3 6 = 5 6 , and B D = 1 5 + 4 8 = 6 3 . (Note that 56 : 63 = 8 : 9)
Therefore, the area of the quadrilateral ABCD = ( 2 1 ) ( 5 6 × 6 3 ) = 1 7 6 4
Moreover, let AE = a, BE = b, CE = c, and DE = d for some numbers a, b, c, d.
We will obtain the system of equations below:
a 2 + b 2 = 2 5 2
b 2 + c 2 = 3 9 2
c 2 + d 2 = 6 0 2
d 2 + a 2 = 5 2 2
Observe that by adding first and third equations: a 2 + b 2 + c 2 + d 2 = 2 5 2 + 6 0 2
And by adding second and fourth: a 2 + b 2 + c 2 + d 2 = 3 9 2 + 5 2 2
Thus, 3 9 2 + 5 2 2 = 2 5 2 + 6 0 2 .
This can be related to British Flag theorem , which deals with summation of squares of distances from a point in a rectangle to its four vertices.