Four Rounders (corrected)
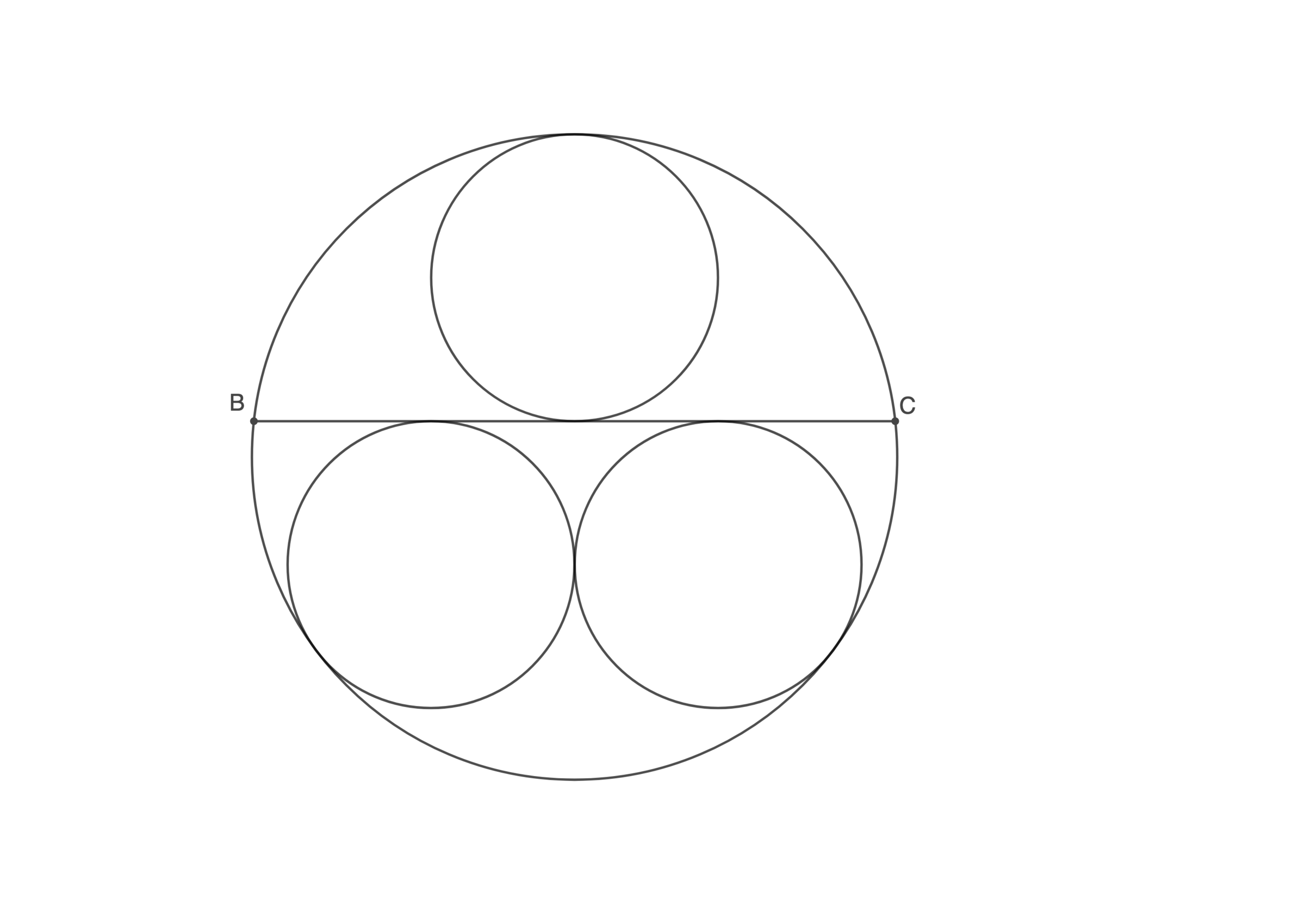
A chord B C is positioned in the unit circle in such a way that the three inner circles are congruent. If the radius of an inner circle is q p , where p and q are coprime positive integers, what is p + q ?
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
It's a coincidence the reversed digits of the given result follows today's date, which is December 3 1 !
That's why I waited until today to post it. :)
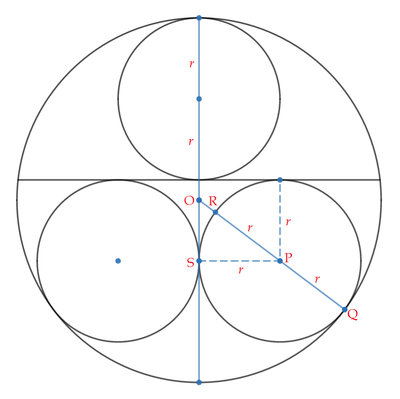
Let the radius of the three congruent circles be r , the centers of the unit circle and the bottom right circle be O and P respectively, and the tangent point of the two circles be Q . Note that the line perpendicular to the tangent line at Q passes through P and O , therefore O , P , and Q are colinear.
Let O Q intersect the circle centered P at R and the tangent point of the bottom two circles be S . By tangent-secant theorem , we have:
O S 2 ( 3 r − 1 ) 2 9 r 2 − 6 r + 1 9 r 2 − 4 r 9 r − 4 ⟹ r = O R ⋅ O Q = ( 1 − 2 r ) ⋅ 1 = 1 − 2 r = 0 = 0 = 9 4 Since r > 0
Therefore p + q = 4 + 9 = 1 3 .
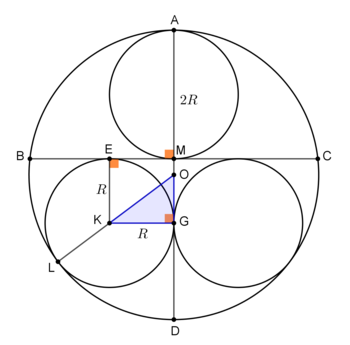 Referring to the figure, points
E
,
M
and
G
are points of contact of the circles and the cords. Let
O
and
K
be the centers of the big circle and the lower-left circle respectively. Let
R
be the radius of the small circles and let
L
be the point of contact of the lower-left circle with the big circle.
Line
A
D
through the center of the upper small circle and the point of contact of the other two small circles is an axis of symmetry of the compound figure of the four circles and cord
B
C
. Hence,
B
C
⊥
A
D
. Also,
K
G
⊥
A
D
.
Referring to the figure, points
E
,
M
and
G
are points of contact of the circles and the cords. Let
O
and
K
be the centers of the big circle and the lower-left circle respectively. Let
R
be the radius of the small circles and let
L
be the point of contact of the lower-left circle with the big circle.
Line
A
D
through the center of the upper small circle and the point of contact of the other two small circles is an axis of symmetry of the compound figure of the four circles and cord
B
C
. Hence,
B
C
⊥
A
D
. Also,
K
G
⊥
A
D
.
Now, O M = O A − A M = 1 − 2 R
O G = M G − O M = E K − O M = R − ( 1 − 2 R ) ⇒ O G = 3 R − 1
O K = O L − K L = 1 − R Using Pythagorean theorem on △ O G K ,
O K 2 = O G 2 + K G 2 ⇔ ( 1 − R ) 2 = ( 3 R − 1 ) 2 + R 2 ⇔ 9 R 2 − 4 R = 0 ⇔ R = 0 R = 9 4 For the answer, p + q = 4 + 9 = 1 3 .
Let r be the radius of an inner circle and label the diagram as follows:
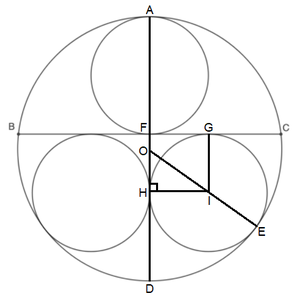
Then H I = r , O I = O E − I E = 1 − r , and O H = F H − O F = G I − ( A O − A F ) = r − ( 1 − 2 r ) = 3 r − 1 .
By the Pythagorean Theorem on △ O H I , r 2 + ( 3 r − 1 ) 2 = ( 1 − r ) 2 , which solves to r = 9 4 for r > 0 . Therefore, p = 4 , q = 9 , and p + q = 1 3 .
Hi David! I just posted my solution, then I refreshed the page and your solution that was already uploaded appeared, same as mine. Happy new year!
I like your solution but am confused as to why OE passes through I.
Log in to reply
O E and I E are radii of the big and small circles , hence, they are both perpendicular to the common tangent to the circles at E . Thus lines O E and I E coincide and points O , I and E are collinear.
Let r denote the radius of an inner circle. Sangaku tells us that the diameter of each of the two adjacent circles is twice the difference of ∣ B D ∣ and ∣ D E ∣ . For this case, if all circles have the common radii, then
2 r r ∣ B D ∣ = 2 ( ∣ B D ∣ − ∣ D E ∣ ) = 2 ( ∣ B D ∣ − 2 r ) = ∣ B D ∣ − 2 r = 3 r
Then, by Pythagorean Theorem, ∣ B D ∣ 2 − ∣ D E ∣ 2 = 5 r . Therefore, the intersecting chord theorem tells us
∣ B E ∣ ⋅ ∣ E C ∣ ( 5 r ) 2 5 r 2 0 0 r = ∣ A E ∣ ⋅ ∣ E D ∣ = ∣ A E ∣ ⋅ ( ∣ A D ∣ − ∣ E D ∣ ) = 2 r ( 2 − 2 r ) = 4 r − 4 r 2 = 4 r − 9 r 2 = r ( 4 − 9 r ) = 9 4 as r is nonzero
So for this problem, p = 4 and q = 9 , giving us p + q = 1 3 .