Four Surprising Semicircles
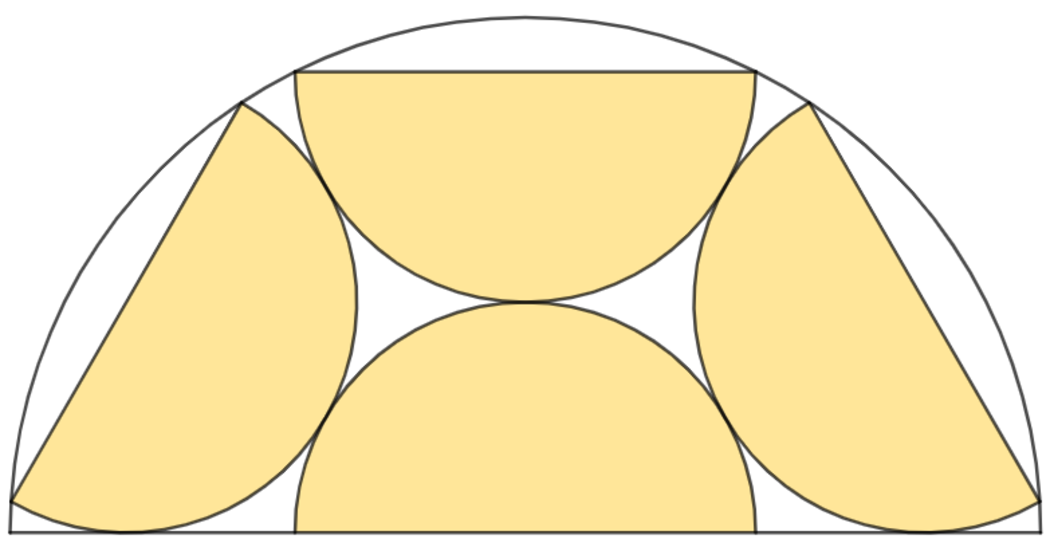
Four identical semicircles are packed inside a larger semicircle as shown above. Find the ratio of the area of four small semicircles to the area of one large semicircle.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Great approach
Log in to reply
Intersecting chords theorem usually save a lot of work.
Just focus on the two smaller semicircles with parallel 'bases'. They can be fitted inside a square with side lengths the same as that base, so the R is the same as the largest V-shape that we can draw in the inscribed square. If we let r = 1, then R² = r² + (2r)² = 1² + 2² = 5. Our ratio is just nr² / R² = (4 × 1²) / (5) = 4/5. All the pies and area formula can be forgotten for a while since all are semicircles (congruency and similarity played their parts) with the important point being area is 2D against length's 1D.
@Michael Huang - It's funny: "None of the given choices" is a (self-excluding) given choice :)
Brilliant approach indeed! Congratulations, sir!
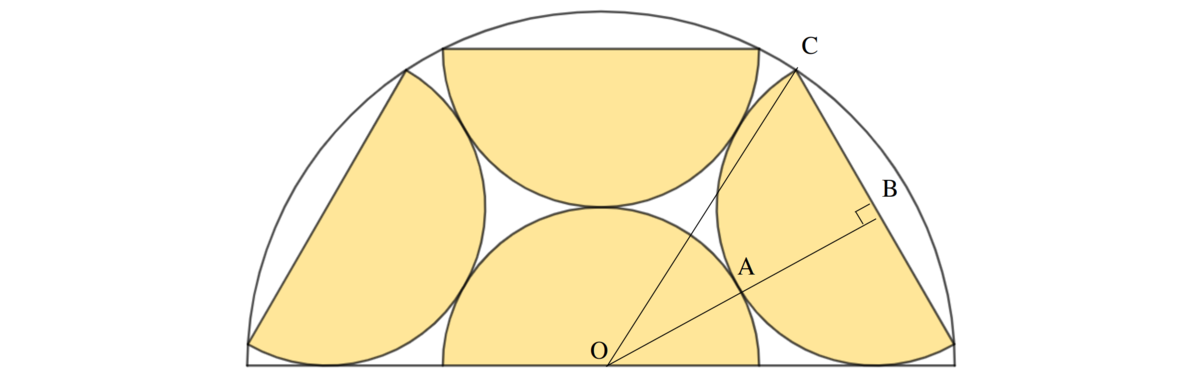
O A = A B = B C hence O C = 2 2 + 1 2 ⋅ O A = 5 ⋅ O A . The area of the large semicircle is 5 times the one of a small semicircle so the yellow area is 5 4 of total area.
Let the center and radius of the large semicircle be O and 1 , the radius of the small semicircle be r , the diameter of the top small semicircle be A B , C E through O bisects A B perpendicularly at D , and C D = k .
We note that C O = C D + D O ⟹ 1 = k + 2 r ⟹ k = 1 − 2 r . By intersecting chords theorem ,
A D ⋅ D B r 2 r 2 ⟹ r 2 = C D ⋅ D E = k ( 2 − k ) = ( 1 − 2 r ) ( 1 + 2 r ) = 1 − 4 r 2 = 5 1 Substituting k = 1 − 2 r
The area ratio is 2 1 π ⋅ 1 2 4 ⋅ 2 1 π r 2 = 4 r 2 = 5 4 .