Four times Four?

A good place to start is a sketch of both sides of the equations in a graph. Clearly, the smallest two solutions belong to negative values of the argument of the absolute value, and the greatest two solutions belong to positive values.

For instance, for the equation $x^2 + 7 = |12x + 20|$ :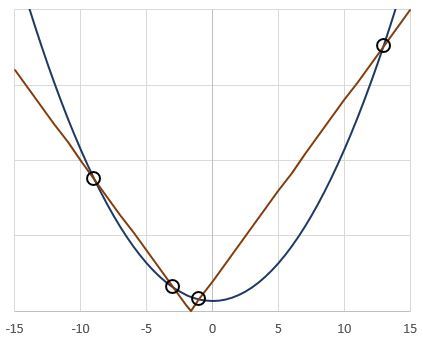

Call the solutions $x_1 < x_2 < x_3 < x_4$ , then the equation can be split out as $\begin{cases} x^2 + ax + (c+b) = 0 & x = x_1,\ x_2 \\ x^2 - ax + (c-b) = 0 & x = x_3,\ x_4 \end{cases}$ For quadratic equations, we know that the linear coefficient is the sum of the solutions (but with a negative sign), and the constant coefficient is their product. That is, $\begin{cases} x_1+x_2 = -a & x_1x_2 = c+b \\ x_3+x_4 = a & x_3x_4 = c-b\end{cases}$ Since $a, b, c$ are positive, we see immediately that $x_1,\ x_2$ must be negative and $x_4$ must be positive.This it the case for all solution sets listed, so we cannot rule anything out yet.

We also that the solutions must satisfy the equation $x_1+x_2+x_3+x_4 = (-a)+a = 0.$ This, sadly, is also the case for all the solution sets listed.

Next consider the combination of $x_1x_2 = c+b$ and $x_3x_4 = c-b$ . Adding them we find $x_1x_2 + x_3x_4 = 2c.$ This implies, first of all, that $x_1x_2 + x_3x_4$ must be positive . This is obviously true if $x_3$ is positive, but if $x_3$ is negative we must check this condition. It turns out that the solution set $\color{#D61F06}{\{-7, -3, -2, 12\}}$ fails this test, since $21 + (-24) < 0$ .

It also implies that $x_1x_2 + x_3x_4$ must be even , since $c$ is an integer. The condition $x_1+x_2+x_3+x_4 = 0$ guarantees that zero, two, or four of the solutions are even; a problem occurs if both $x_1, x_2$ are even and $x_3, x_4$ are odd, or vice versa.

Thus we can rule out the sets $\color{#D61F06}{\{-4, -2, -1, 7\}}$ and $\color{#D61F06}{\{-8, -2, -1, 11\}}$ as they are even-even-odd-odd. (Don't be fooled by the order in which the numbers are listed!)

We find that the only candidate for the solution is $\boxed{\color{#3D99F6}{\{-8, -7, 2, 13\}}}$ . It is straightforward to calculate that $a = 15,\ b = 15,\ c = 41$ so that the corresponding equation is $\color{#3D99F6}{x^2 + 41 = |15x+15|\ \ \ \therefore\ \ \ x\in\{-8, -7, 2, 13\}}.$

Note that if we remove the condition that $c$ is an integer, we also have $\color{#D61F06}{x^2 + \tfrac12 = |8x+7\tfrac12|\ \ \ \therefore\ \ \ x\in\{-4, -2, -1,\ 7\} \\ x^2 + 2\tfrac12 = |10x+13\tfrac12|\ \ \ \therefore\ \ \ x\in\{-8, -2, -1, 11\}}.$