B A B C
Let A B C be a right-angled triangle right angled at B . Suppose E and F are the midpoints of A B and A C respectively. It is also given that incentre of △ A B C lies on the circumcircle of △ A E F .
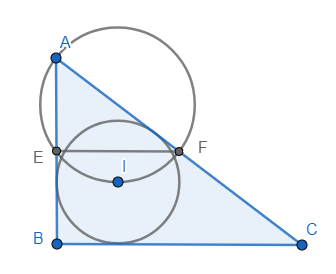
Find the ratio B A B C .
If the ratio can be written as b a , where a , b are coprime positive integers, find the product a b .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Nice and precise Solution
How do you get EF/2= r ? I need a proof
Log in to reply
The proof will take time as you have to consider the concepts related to chords and tangents, but I have a simple solution for you. Drop a perpendicular from F to BC. It will touch the in-circle at a point (in the form of a tangent) such that EF is equal to the diameter of the in-circle passing through the centre I.
From the image provided, let ∣ I P ∣ ⊥ ∣ A F ∣
Let ∣ F P ∣ = p , ∣ A F ∣ = 2 R , then ∣ P F ∣ = 2 R − p
A F is the diameter, so ∠ A I F = 9 0 ∘
Δ A I P ∼ Δ I F P
Let ∣ I P ∣ = r ,
then, p ( 2 R − p ) = r 2
E , F are midpoints of A B , A C respectively.
A C = 4 R
Let midpoint of A F be M
Let M Q ⊥ A E
Let ∣ A Q ∣ = x
∣ A B ∣ = 4 x
∣ M Q ∣ = R 2 − x 2
∣ B C ∣ = 4 R 2 − x 2
Let I X ⊥ A B
∣ A X ∣ = p
∣ B X ∣ = 4 x − p
∣ B X ∣ = r
4 x − p = r
Similiarly, we have 4 R 2 − x 2 − r = 4 R − p
( 1 ) : p ( 2 R − p ) = r 2
( 2 ) : 4 x − p = r
( 3 ) : 4 R 2 − x 2 − r = 4 R − p
From ( 2 ) , p = 4 x − r
( 3 ) : 4 R 2 − x 2 − r = 4 R − 4 x + r
4 R 2 − x 2 − 2 r = 4 R − 4 x
2 R 2 − x 2 − r = 2 ( R − x )
2 R 2 − x 2 − 2 ( R − x ) = r
r = 2 R − x ( R + x − R − x )
( 2 ) : p = 4 x − r
p = 4 x − 2 R − x ( R + x − R − x )
p = 4 x − 2 R 2 − x 2 + 2 ( R − x )
p = 2 R + 2 x − 2 R 2 − x 2
p = 2 R + x ( R + X − R − x )
( 1 ) : p ( 2 R − p ) = r 2
2 R p − p 2 = r 2
2 R ⋅ 2 R + x ( R + X − R − x ) − [ 2 R + x ( R + X − R − x ) ] 2 = [ 2 R − x ( R + x − R − x ) ] 2
4 R ⋅ R + x ( R + X − R − x ) − 4 ( R + x ) ( R + X − R − x ) 2 = 4 ( R − x ) ( R + x − R − x ) 2
4 R ⋅ R + x ( R + X − R − x ) = 4 ( R + x + R − x ) ( R + x − R − x ) 2
4 R ⋅ R + x ( R + X − R − x ) = 4 ( 2 R ) ( R + x − R − x ) 2
R + x ( R + X − R − x ) = 2 ( R + x − R − x ) 2
R + x = 2 ( R + x − R − x )
R + x = 2 R + x − 2 R − x )
R + x = 2 R − x
R + x = 4 ( R − x )
3 R = 5 x
R x = 5 3
∣ A M ∣ ∣ A Q ∣ = 5 3
∣ A C ∣ ∣ A B ∣ = 5 3
∣ B A ∣ ∣ B C ∣ = 3 4 = b a
a b = 4 × 3 = 1 2
It is very tricky to juggle with three variables R , r , x at the beginning and R + x and R − x at the end. It appeals so much to me how algebraic this geometry problem is!
Very nice solution. Yes,i too feel its more of algebra than geometry.
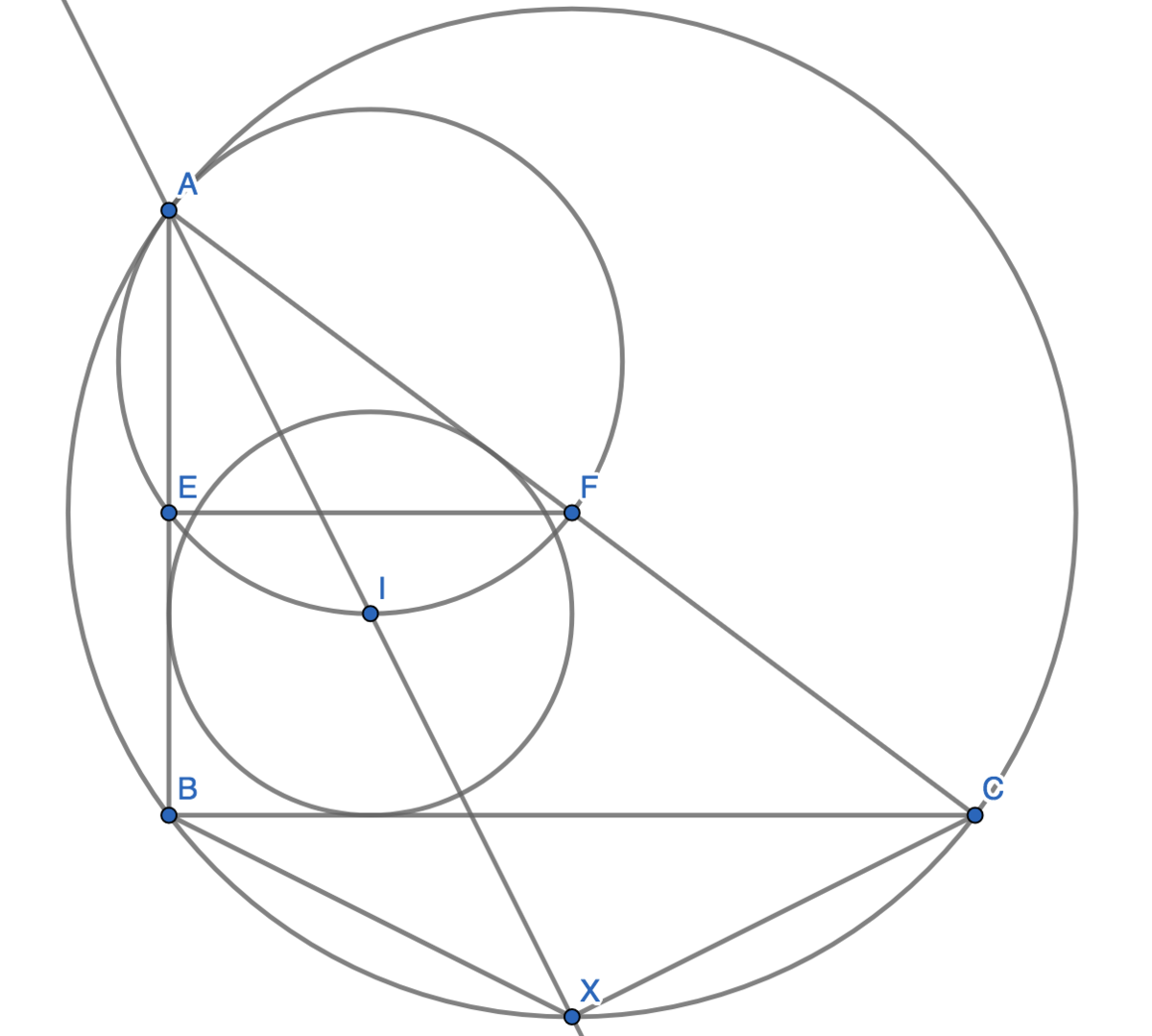
Let ω 1 be the circumcircle of △ A E F and ω 2 be the circumcircle of △ A B C . It is clear that there exists a homothety that maps △ A E F to △ A B C and ω 1 to ω 2 with dilation ratio 2. Letting X be the intersection of line A I with ω 2 , we have A X = 2 A I by the homothety, so A I = I X .
Let a = B C , b = A C , c = A B , and n = I X . It is well-known that I X = B X = C X , so B X = C X = n and A X = 2 n . Applying Ptolemy's Theorem on A B X C yields
A B ( C X ) + A C ( B X ) c n + b n c + b = B C ( A X ) = a ( 2 n ) = 2 a . ( ∗ )
We also have a 2 + c 2 = b 2 by the Pythagorean Theorem, and we wish to find c a . From equation ( ∗ ) , we get b = 2 a − c . Substituting this into our Pythagorean Theorem equation yields
a 2 + c 2 a 2 + c 2 3 a 2 − 4 a c a ( 3 a − 4 c ) = ( 2 a − c ) 2 = 4 a 2 − 4 a c + c 2 = 0 = 0 .
Since a = 0 , we must have 3 a − 4 c = 0 , or c a = 3 4 . Our final answer is 4 ( 3 ) = 1 2 .
i just used coordinates. if we take B to be the origins, then the in-centre has coordinates ( r , r ) with r = 2 x + y − x 2 + y 2 where x,y are side lengths. the circumcentre of the smaller triangle has coordinates ( 3 / 4 x , 1 / 4 y ) with circumradius R = 4 x 2 + y 2 . we can now use the equation of a circle to get ( 3 / 4 x − r ) 2 + ( 1 / 4 y − r ) 2 = R 2 = 1 6 x 2 + y 2 → x 2 − 3 x r − y r + 4 r 2 = 0 → 1 − 3 x r − x y x r + 4 ( x r ) 2 = 0 if we define x y = a , then x r = 2 1 + a − 1 + a 2 . plugging this in and expanding everything: 3 + 3 a 2 − 1 + a 2 − 3 a 1 + a 2 = 0 → 3 ( 1 + a 2 ) = ( 3 a + 1 ) a 2 + 1 → 9 ( 1 + a 2 ) = ( 3 a + 1 ) 2 → 9 = 6 a + 1 → a = 3 4
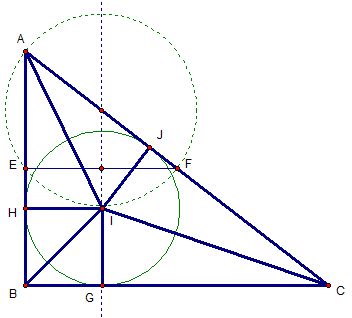
You hardly need the circumcircle except to note it lies on the perpendicular bisector of E F and contains I . Let the points of tangency of the incircle be as shown and connected to the incenter.
B G = 2 1 E F = 4 1 B C . For simplicity let B G = 1 , B C = 4 , G C = 3 .
Let B A = x so A C = 1 6 + x 2 . and A H = x − 1 .
Then by congruent triangles B H = 1 , A H = A J = x − 1 , C G = C J = 3 which gives another expression for A C : x + 2
Solving 1 6 + x 2 = ( x + 2 ) 2 gives x = 3 so B A B C = 3 4 and the solution is then 4 ⋅ 3 = 1 2
Let A B = a , B C = b and A C = c .
I will not go into the rigor of proving the theorem about in-circles in a right angled triangle, but it is well known that the in-radius, r = 2 a + b − c
Looking at the bigger circle w.r.t the in-circle, we realize that r = 2 E F ⟹ E F = a + b − c
Now considering two right angled triangles, A B C and A E F , we get two equations.
A C 2 = A B 2 + B C 2 ⟹ c 2 = a 2 + b 2 ... (i)
A F 2 = A E 2 + E F 2 ⟹ ( 2 c ) 2 = ( 2 a ) 2 + ( a + b − c ) 2 ... (ii)
Using (i) and (ii), we get: c = a + 2 b ... (iii)
Substituting (iii) back in (i), we get: a b = B A B C = 3 4
Hence, the solution sought = 4 × 3 = 1 2
You do not have to scratch your head or go through elaborate theorems or extensive calculations, if you know the in-radius relationship.