Fractal Area

Consider one of the "arms" of the fractal square:

Call the blue area within this arm $x.$ Then the fraction of the larger square that is blue is:

$B=4x+\frac{1}{9}$

Now consider that if we remove the two blue squares that are each $\frac{1}{81}$ of the larger square, we end up with three "arms" that are similar to the original arm shape, except they are each $\frac{1}{9}$ its size.

Thus, we can write an equation for $x$ recursively:

$x-\frac{2}{81}=\frac{1}{3}x$

Solving this for $x$ gives $\frac{1}{27}.$ Now returning to our equation for fraction of blue area:

$\begin{aligned} B &= 4x + \frac{1}{9} \\ &= \frac{4}{27}+\frac{1}{9} \\ &= \boxed{\frac{7}{27}}. \end{aligned}$

Considering the reduction of the blue area by stages as follows:

$\begin{aligned} A_{\color{#3D99F6}blue} & = 1 - \frac 49 - \frac 4{9^2} \times 4 - \frac 4{9^3} \times 4 \times 3 - \frac 4{9^4} \times 4 \times 3^2 - \frac 4{9^5} \times 4 \times 3 ^3 - \cdots \\ & = 1 - \frac 49 - \frac {16}{3^4} - \frac {16}{3^5} - \frac {16}{3^6} - \frac {16}{3^7} - \cdots \\ & = 1 - \frac 49 - \frac {16}{3^4} \sum_{k=0}^\infty \frac 1{3^k} \\ & = 1 - \frac 49 - \frac {16}{3^4} \left(\frac 1{1-\frac 13}\right) \\ & = 1 - \frac 49 - \frac {16}{3^4} \times \frac 32 \\ & = 1 - \frac 49 - \frac 8{27} \\ & = \boxed{\dfrac 7{27}} \end{aligned}$

The fraction of the larger square that is shaded orange is $O = \frac{4}{9} + \frac{16}{81} + \frac{48}{729} + \frac{144}{6561} \dots$

Except for the first term $\frac{4}{9}$ , the other terms follow the geometric sequence $x = \frac{16}{81} + \frac{48}{729} + \frac{144}{6561} \dots = \frac{16}{81} + \frac{3}{9}(\frac{16}{81} + \frac{3}{9}(\frac{16}{81} \dots$ .

Substituting x into itself gives $x = \frac{16}{81} + \frac{3}{9}x$ and solves to $x = \frac{8}{27}$ .

Therefore, the fraction of the larger square that is shaded orange is $O = \frac{4}{9} + x = \frac{4}{9} + \frac{8}{27} = \frac{20}{27}$ .

The fraction of the larger square that is shaded blue must then be $B = 1 - O = 1 - \frac{20}{27} = \boxed{\frac{7}{27}}$ .

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

# https://brilliant.org/weekly-problems/2018-03-12/intermediate/?p=2
from fractions import Fraction
from math import sqrt

square = int(raw_input("How many identical squares (ex. 4,9,16...)?: ")) # ex. 9
sq = [x**2 for x in range(2,100,1)]
while square not in sq:
    square = int(raw_input('Please try again: '))

sections = int(raw_input("How many sections altered (some value < than number of identical squares?: ")) # ex. 4
x = [x for x in range(1,square+1)]
while sections not in x:
    sections = int(raw_input('Please try again: '))

sign = int(raw_input("How many squares altered in iteration 1?: "))  #     "+" sign   =  4
while sign not in x[:-1]:
    sign = int(raw_input('Please try again: '))


x = 1 - (float(sign)/square) - sum((float(sign)*sections) / sqrt(square)**(k+sqrt(square)) for k in range(1, 200))
print '\n\nFraction of the larger square shaded blue as pattern continues indefinitely = %s' \
    % Fraction(x).limit_denominator(1000)

Fraction of the larger square shaded blue as pattern continues indefinitely = 7/27

$\;\;\;\;\;\;\boxed{\frac{1}{9}\;}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;4\;\;\times\;\;\boxed{\frac{2}{9^{2}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;4\;\;\times\;\;3\;\;\times\;\;\boxed{\frac{2}{9^{3}}}\;\;\;\;\;\;\;\;\;+\;\;4\times3\times3\times\boxed{\frac{2}{9^{4}}}\;\;+\;\;.\;\;.\;\;.$

$\boxed{ \begin{array} {l l} \text{- Consider the red boxes as incremental blue shade fraction of the larger square under each iteration, } \\ \text{ whose corresponding fractional values are the boxed ones beneath each. } \end{array} }$

$\therefore\;$ for each fractal pattern growth cycle iterated progressively, ${\color{#3D99F6}Fractional\;Growth}, F_{i}=\frac{{3^{i-2}}\times2}{9^{i}},\; \forall \; i \geq 2,\;\text{for each branch(4 in total) from the central node}\;\left ( \frac{1}{9} \right )\;on\; i^{th}\; iteration;$

$\therefore\;$ the corresponding infinite sum associated with this pattern is, $\begin{aligned} F&=\left ( \frac{1}{9} \right )+\left ( \frac{4\times2}{9^{2}} \right )+\left ( \frac{4\times3\times2}{9^{3}} \right )+\left ( \frac{4\times3\times3\times2}{9^{4}} \right )+\left ( \frac{4\times3\times3\times3\times2}{9^{5}} \right )+\;.\;.\;.\;\\ &=\left ( \frac{1}{9} \right )+\left ( \frac{2^{3}}{9^{2}} \right )+\left ( \frac{2^{3}\times3}{9^{3}} \right )+\left ( \frac{2^{3}\times3^{2}}{9^{4}} \right )+\left ( \frac{2^{3}\times3^{3}}{9^{5}} \right )+\;.\;.\;.\;\\ &=\left ( \frac{1}{9} \right )+\left [ \left ( \frac{2^{3}}{9^{2}} \right )\left ( 1+\frac{3}{9}+\frac{3^{2}}{9^{2}}+\frac{3^{3}}{9^{3}}+\;.\;.\;.\;\right ) \right ]\\ &=\left ( \frac{1}{9} \right )+\left [ \left ( \frac{2^{3}}{9^{2}} \right )\left ( 1+\frac{1}{3}+\frac{1}{3^{2}}+\frac{1}{3^{3}}+\;.\;.\;.\;+\frac{1}{3^{\infty }}\right ) \right ]\\ \end{aligned}$ $\boxed{{\color{#D61F06}\sum_{k=0}^{\infty}\left ( \frac{1}{3^{k}} \right )=\frac{3}{2}}}$ $\because\boxed{ \begin{array} {l l} \text{the sum of reciprocals of powers of any n produce a convergent geometric series: 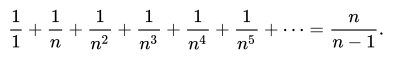} \end{array} }$ $F= \left ( \frac{1}{9} \right )+\left [ \left ( \frac{2^{3}}{3^{4}} \right )\left ( \frac{3}{2}\right ) \right ]=\left ( \frac{1}{9} \right )+\left (\frac{2^{2}}{3^{3}}\right)=\frac{1}{9}+\frac{4}{27}=7/27$

$-µτΣ$