Fractal Fraction

It is important to first note that the sum of the lengths of the top sides of the squares will always be 1.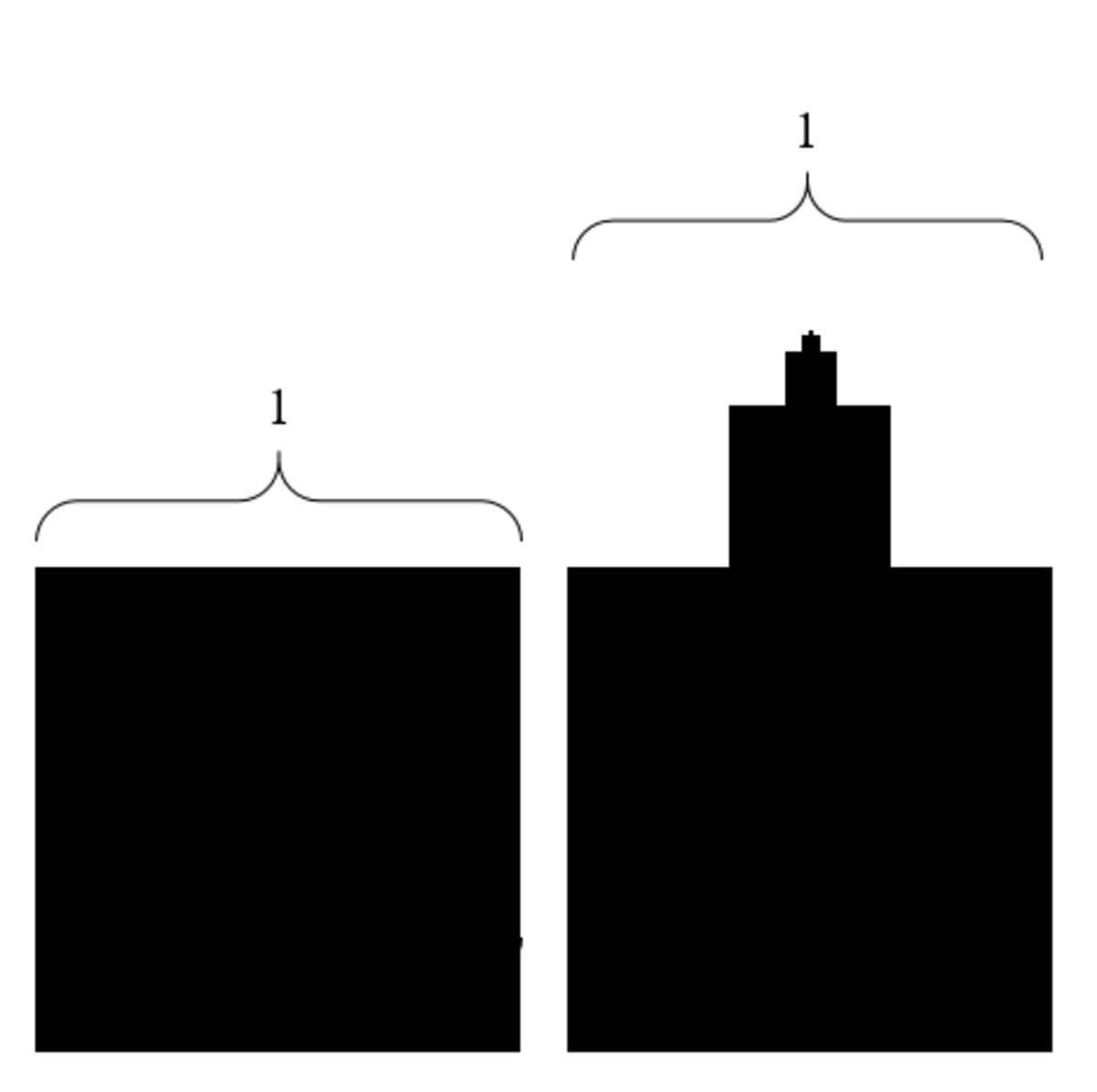 From there, it can be seen that the perimeter of the shape is equal to 4 + $\frac{2}{3}$ + $\frac{2}{9}$ ...

S = $\frac{2}{3}$ + $\frac{2}{9}$ + $\frac{2}{27}$ ...

3S = 2 + $\frac{2}{3}$ + $\frac{2}{9}$ + $\frac{2}{27}$ ...

2S = 2

S = 1

Therefore the perimeter of the fractal is equal to 4 + 1 = 5 .

The area of the fractal is 1 + $\frac{1}{9}$ + $\frac{1}{81}$ ...

Another series summation can be used to solve this.

S = 1 + $\frac{1}{9}$ + $\frac{1}{81}$ ...

9S = 9 + 1 + $\frac{1}{9}$ + $\frac{1}{81}$ ...

8S = 9

S = $\frac{9}{8}$

So the ratio is 5 to $\frac{9}{8}$ . This can multiplied out by 8 to give a nice integer ratio, and arrive at the final answer of 40:9 .

The area after $n$ interactions may be written as

$A_n = 1 + \left( \frac{1}{3} \right)^{2} + \left( \frac{1}{3} \cdot \frac{1}{3} \right)^{2} + \cdots + \left( \overbrace{\frac{1}{3} \cdots \frac{1}{3}}^{n \; \text{times}} \right)^{2} = \sum_{i=0}^{n} \left( \frac{1}{3} \right)^{2i} = \frac{1 - \left( \frac{1}{9} \right)^{n+1}}{1 - \frac{1}{9}} = \frac{9 - \left( \frac{1}{9} \right)^n}{8},$

which will clearly give us $A_n \xrightarrow{n \rightarrow \infty} 9/8$ . For the perimeter

$P_n = 4 + \left( - \frac{1}{3} + \frac{3}{3} \right) + \left( - \frac{1}{3} \cdot \frac{1}{3} + \frac{3}{3} \cdot \frac{1}{3} \right) + \cdots + \left( - \overbrace{\frac{1}{3} \cdots \frac{1}{3}}^{n \; \text{times}} + \frac{3}{3} \cdot \overbrace{\frac{1}{3} \cdots \frac{1}{3}}^{n-1 \; \text{times}} \right) = 4 + \sum_{i=0}^{n-1} \left( \frac{1}{3} \right)^{i} - \sum_{i=1}^{n} \left( \frac{1}{3} \right)^{i},$

which actually shows us that

$P_n = 5 - \left( \frac{1}{3} \right)^{n} \xrightarrow{n \rightarrow \infty} 5.$

We want

$\left( \frac{P_n}{A_n} \right )_{n \rightarrow \infty} = \frac{5}{9/8} = \frac{40}{9}.$

The Perimeter = 3 + 4/3 + 4/9 + 4/27 + ..... = 3 + (4/3)/(1 – 1/3) = 5. The Area = 1 + 1/9 + 1/81 + .... = 1/(1 – 1/9) = 9/8. The ratio of P/A = 5/(9/8) = 40/9.