Fractal Graph?!

Calculus Level 3

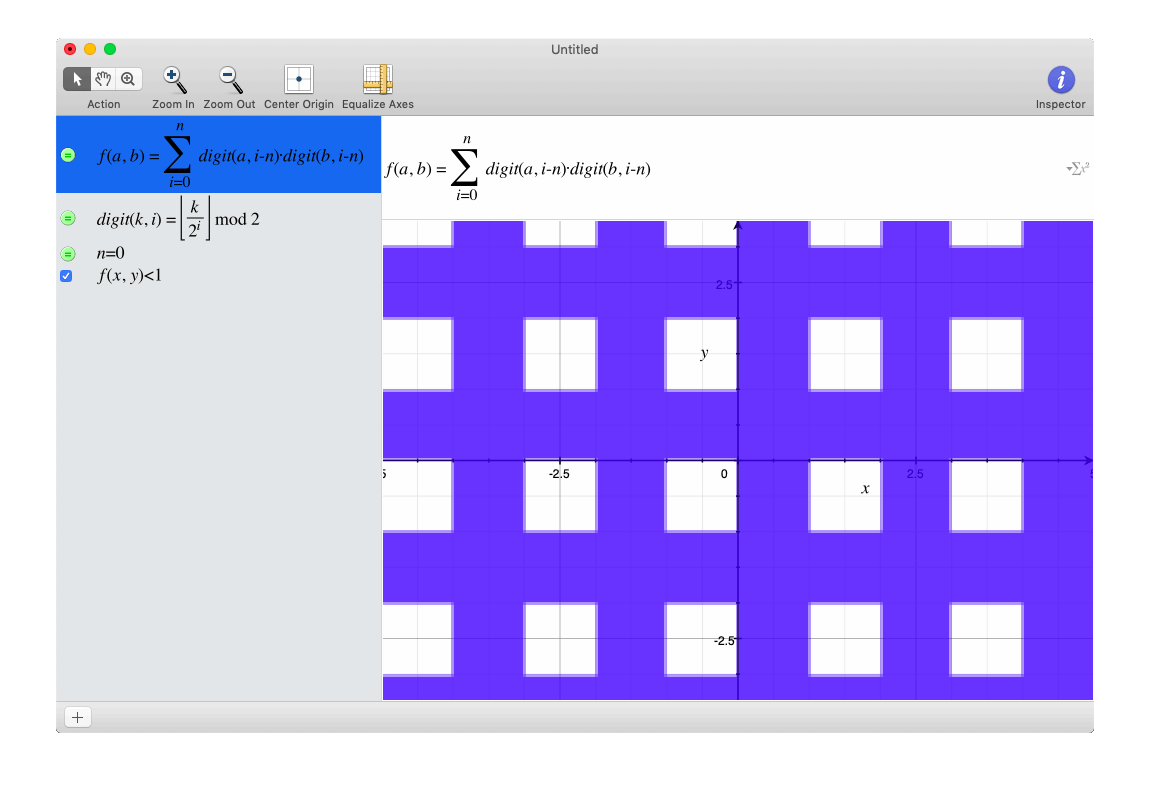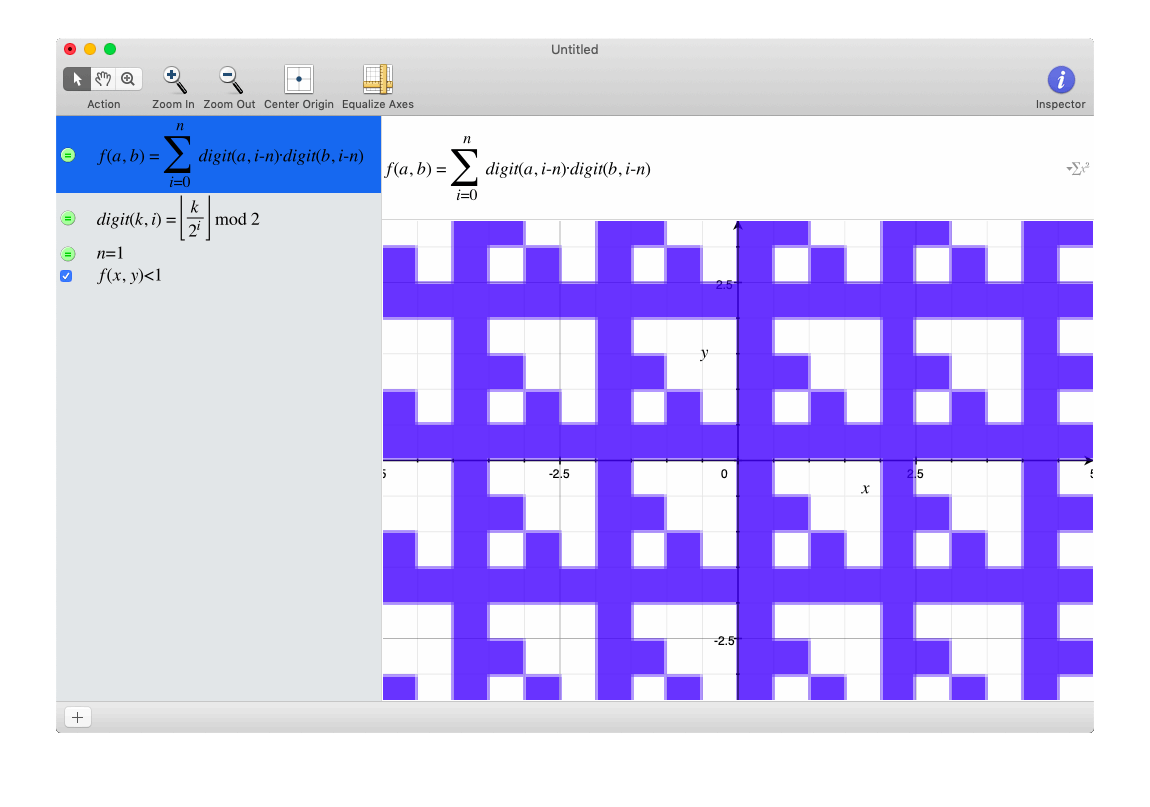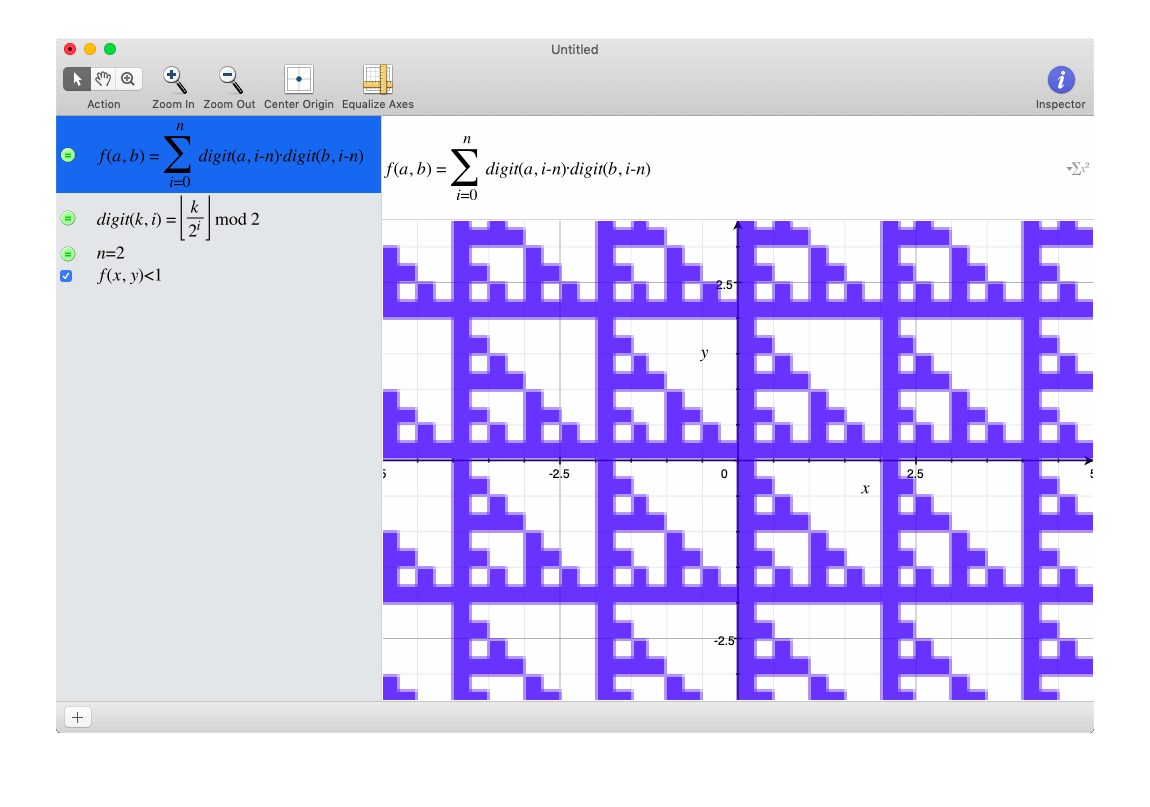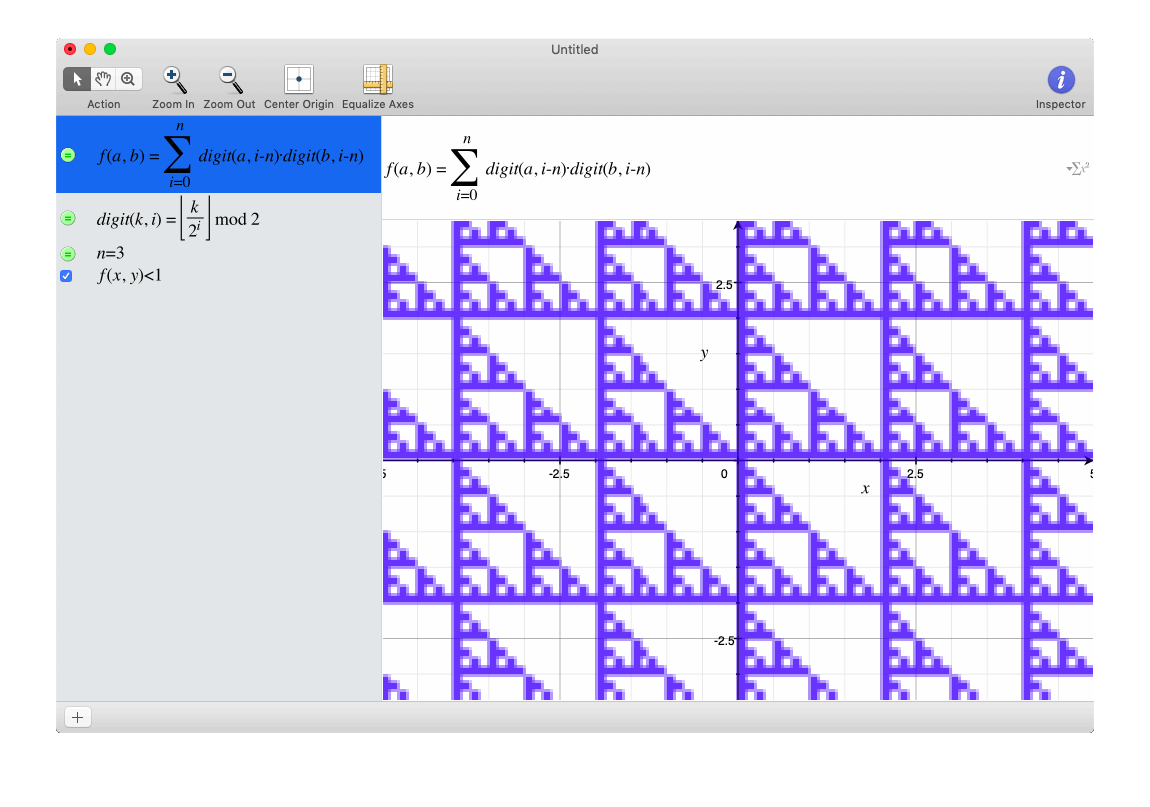
Try graphing the inequality

lim ⁡ n → ∞ ( ∑ i = 0 n digit ( x , i − n ) ⋅ digit ( y , i − n ) ) < 1 \displaystyle {\lim_{n\to\infty}\left(\sum\limits_{i=0}^n{\text{digit}(x, i-n)\cdot{}\text{digit}(y, i-n)}\right)<1}

where digit ( k , i ) { \text{digit}(k, i)} is the i'th digit of a right of the decimal point in base 2. (i.e. digit ( k , i ) = ⌊ k 2 i ⌋ m o d 2 {\text{digit}(k, i)=\lfloor{\frac{k}{2^i}\rfloor}\mod 2}

Notice anything? What is the fractal dimension of this shape (in the range, x ∈ [ 0 , 1 ) x\in[0, 1) and y ∈ [ 0 , 1 ) y\in[0, 1) ?

log₂(3) about 1.3058 π

Chase Marangu by chase marangu , 21, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Chase Marangu
Mar 1, 2020

on the interval x ∈ [ 0 , 1 ) ∩ y ∈ [ 0 , 1 ) x\in[0, 1)\cap y\in[0, 1) the limiting point set is a linear-transformed sierpinski triangle. Scaling it up by 2x side length increases it's "fractal mass" by 3x (as there are 3x as many sierpinski triangles) Therefore the answer is l o g 2 ( 3 ) log_2{(3)} . Analogously scaling up a square by 2x side length gives 4x as many squares of original side length so l o g 2 ( 4 ) = 2 log_2{(4)}=2 and for cube l o g 2 ( 8 ) = 3 log_2{(8)}=3

2 Helpful 1 Interesting 2 Brilliant 2 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...