Fractal Iteration Area
The figure below shows the first three iterations.
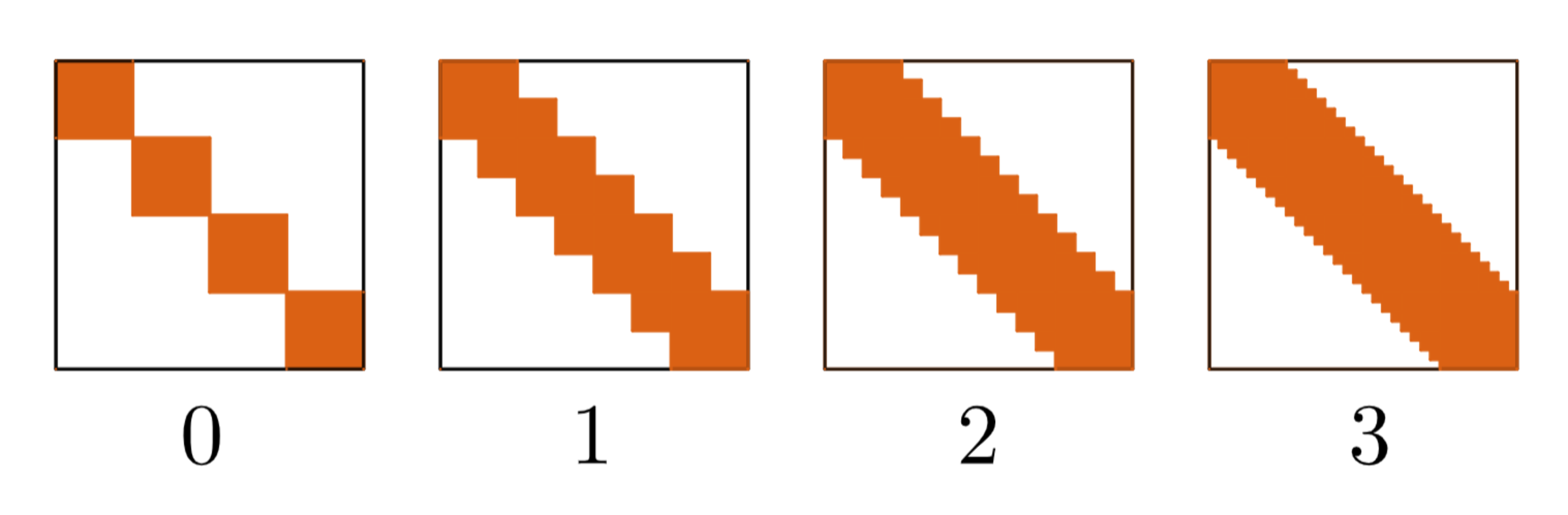
After infinitely many iterations, the fraction of the colored area can be expressed as b a , where a and b are positive coprime integers. Find a + b .
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
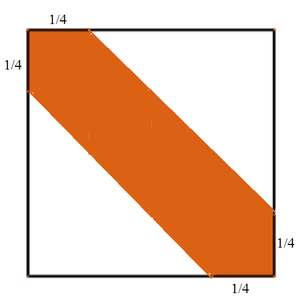
After infinitely many iterations, the final colored and uncolored (white) areas is as shown above. Let the large square be a unit square. Then the final white area is ( 4 3 ) 2 and the final colored area is 1 − ( 4 3 ) 2 = 1 − 1 6 9 = 1 6 7 . Therefore a + b = 7 + 1 6 = 2 3 .
The final colored area is 1 - (3/4)^2 A small typo Please correct.
The first iteration has 4 squares, and after many iterations, the following 6 pink triangles will be added:

The total area is then 4 ⋅ ( 4 1 ) 2 + 6 ⋅ 2 1 ⋅ ( 4 1 ) 2 = 1 6 7 , so a = 7 , b = 1 6 , and a + b = 2 3 .
In this figure, it expands 3 times with each iterations(The blue area is the default).
Then use geometric series to solve:
A = 4 1 + 2 5 3 + 2 6 3 + 2 7 3 + … = 4 1 + n = 5 ∑ ∞ 2 n 3 = 4 1 + 1 − 2 1 3 2 3 = 1 6 7
Therefore, the answer is 7 + 1 6 = 2 3 .