Fractal Maze

Logic Level 2

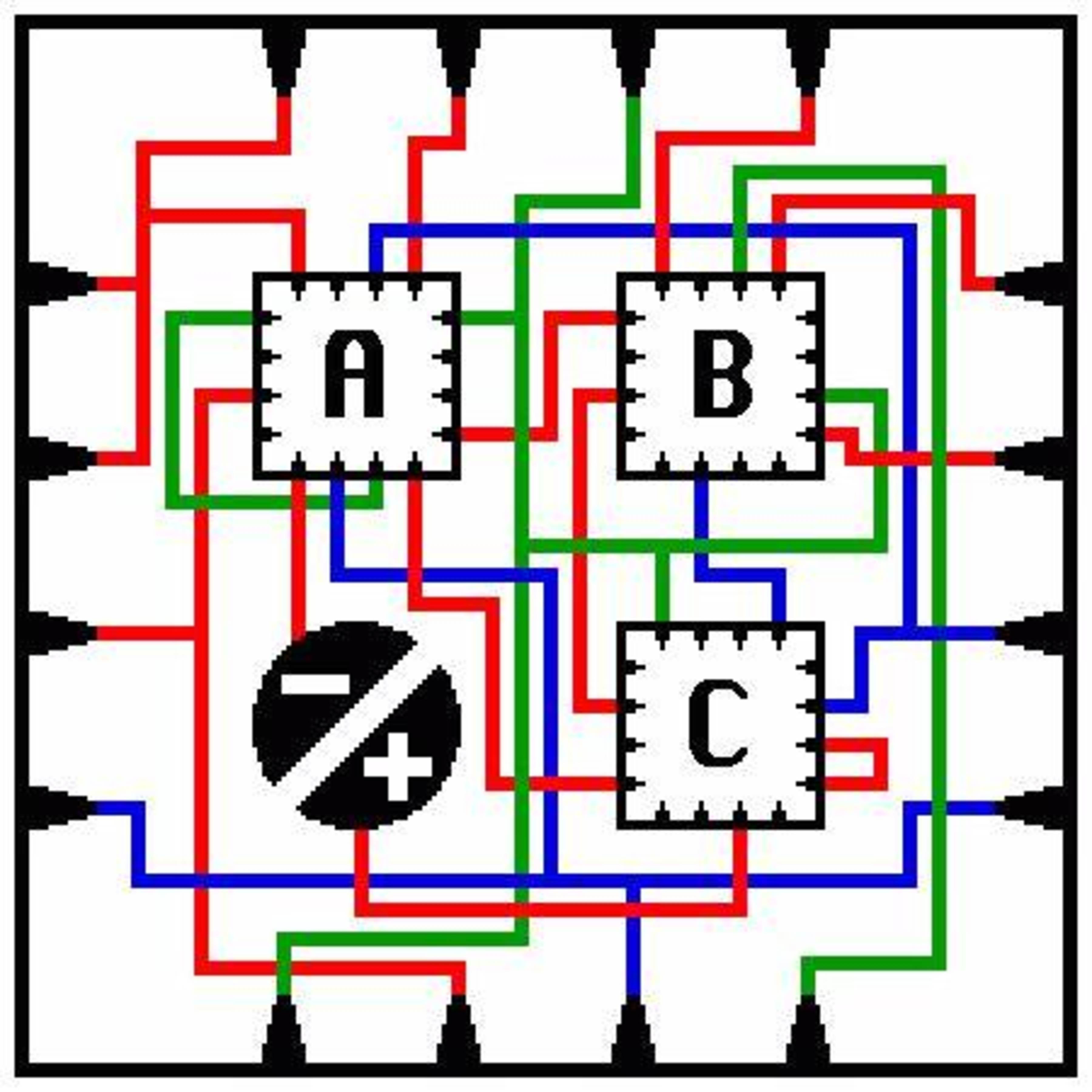
Above is the fractal maze , where region A , B , C A,B,C are exact copies of the maze itself. Is it possible to go from + + sign to − - sign (of the same depth as the starting point)?

Note: You can't go from one path to another by the intersections. These are actually high-way overpasses.

No Yes

Alice Smith by Alice Smith , 20, China

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

David Vreken
May 20, 2020

1 Helpful 0 Interesting 0 Brilliant 0 Confused

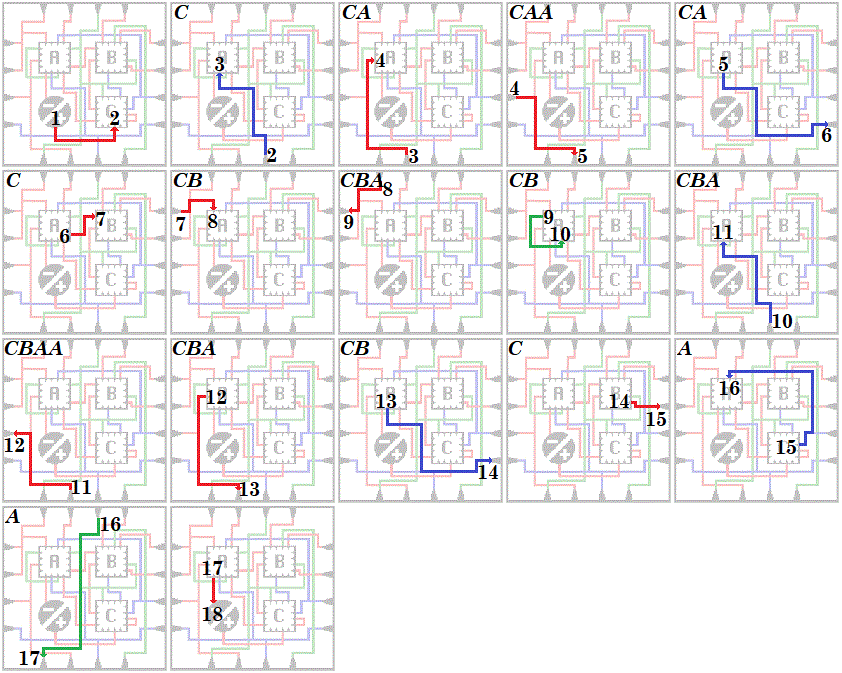
Wow, easy approach! But I think there is something wrong here. I meant the negative sign of the same depth as the positive sign.

Alice Smith - 1 year ago

The - sign that you enter is not at the same depth as the + sign you leave. You are still in the C square when you enter the -sign.

Joshua Lowrance - 1 year ago

Log in to reply

Hmmm ... that stipulation was not in the original problem. I'll have to look at this again.

David Vreken - 1 year ago

Log in to reply

Okay, I updated my solution.

David Vreken - 1 year ago

@David Vreken , Similar reasoning. By the way, @Alice Smith Fantastic problem. The most unique one I've seen in a while. A whole new concept like a fractal in a maze is just awesome!!

Mahdi Raza - 1 year ago

Log in to reply

Yeah, I just found it on the Internet and decided to post it here. Actually, it's a very good problem!

Alice Smith - 1 year ago

Ohh, can you please share the original link. Thanks!

Mahdi Raza - 1 year ago

Log in to reply

http://www.mathpuzzle.com/18Nov2003.html

Alice Smith - 1 year ago

Nice thank you for sharing another resource! The article itself has another hard fractal puzzle. I'll try to solve it!

Mahdi Raza - 1 year ago

I wrote this Python computer program to help me find the solution: 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
 
# Fractal Maze
# Python

# set up variables
D = []
NA = []
NB = []
NC = []
for a in range(0, 17):
    D.append([])
    NA.append([])
    NB.append([])
    NC.append([])

# set up pathway choices
# Key:
#    12 11 10 09
# 13             08
#
# 14             07
#
# 15             06
#
# 16             05
#    01 02 03 04

D[0] = []
D[1] = ["A08", "10", "C12", "B06"]
D[2] = ["15", "A15"]
D[3] = ["16", "05", "A02"]
D[4] = ["B10"]
D[5] = ["03", "16", "A02"]
D[6] = ["C07", "A10"]
D[7] = ["B05"]
D[8] = ["B09"]
D[9] = ["B12"]
D[10] = ["A08", "01", "C12", "B06"]
D[11] = ["A09"]
D[12] = ["A12", "13", "14"]
D[13] = ["A12", "12", "14"]
D[14] = ["A12", "12", "13"]
D[15] = ["A15", "02"]
D[16] = ["03", "05", "A02"]

NA[0] = []
NA[1] = ["-"]
NA[2] = ["16", "03", "05"]
NA[3] = ["A13"]
NA[4] = ["C16"]
NA[5] = ["B13"]
NA[6] = []
NA[7] = []
NA[8] = ["10", "01", "C12", "B06"]
NA[9] = ["11"]
NA[10] = ["06", "C07"]
NA[11] = []
NA[12] = ["12", "13", "14"]
NA[13] = ["A03"]
NA[14] = []
NA[15] = ["02"]
NA[16] = []

NB[0] = []
NB[1] = []
NB[2] = ["C09"]
NB[3] = []
NB[4] = []
NB[5] = ["07"]
NB[6] = ["01", "10", "A08", "C12"]
NB[7] = []
NB[8] = []
NB[9] = ["08"]
NB[10] = ["04"]
NB[11] = []
NB[12] = ["09"]
NB[13] = ["A05"]
NB[14] = []
NB[15] = ["C14"]
NB[16] = []

NC[0] = []
NC[1] = []
NC[2] = []
NC[3] = ["+"]
NC[4] = []
NC[5] = ["C06"]
NC[6] = ["C05"]
NC[7] = ["06", "A10"]
NC[8] = []
NC[9] = ["B02"]
NC[10] = []
NC[11] = []
NC[12] = ["B06", "01", "A08", "10"]
NC[13] = []
NC[14] = ["B15"]
NC[15] = []
NC[16] = ["A04"]

# function that takes in a path sequence and returns a list of
#   possible next path sequences ("~" means "leaving")
def g(s):
    tilde = (s[-4:-3] == "~")
    letter = s[-3:-2]
    number = int(s[-2:])
    if tilde:
        unaff = s[:-5]
        pletter = s[-5:-4]
    else:
        unaff = s[:-4]
        pletter = s[-4:-3]
    nstr = []
    rstr = []
    if tilde:
        if letter == "A":
            for a in range(0, len(NA[number])):
                nstr.append(NA[number][a])
        elif letter == "B":
            for a in range(0, len(NB[number])):
                nstr.append(NB[number][a])
        elif letter == "C":
            for a in range(0, len(NC[number])):
                nstr.append(NC[number][a])
        for a in range(0, len(nstr)):
            if len(nstr[a]) == 1:
                rstr.append("")
            elif len(nstr[a]) == 2:
                rstr.append(unaff + "~" + pletter + nstr[a])
            elif len(nstr[a]) == 3:
                rstr.append(unaff + pletter + nstr[a])
    else:
        for a in range(0, len(D[number])):
            nstr.append(D[number][a])
        for a in range(0, len(nstr)):
            if len(nstr[a]) == 1:
                rstr.append("")
            elif len(nstr[a]) == 2:
                rstr.append(unaff + pletter + "~" + letter + nstr[a])
            elif len(nstr[a]) == 3:
                rstr.append(unaff + pletter + letter + nstr[a])
    for a in range(0, len(nstr)):
        if len(rstr[a]) > 0:
            if rstr[a][0] == "~" and not (
                rstr[a][1] == "A" or rstr[a][1] == "B" or rstr[a][1] == "C"):
                rstr[a] = ""
    return rstr

# Go through each path sequence starting from "C03" until "~A01" is found.
#   The p list keeps track of each possible path sequence by string,
#   index sequence, and number of moves: p[moves][(path string, path seq)]
m = 0
p = []
p.append([])
p[0].append(("C03", ""))
fs = ""
while fs == "":
    m += 1
    p.append([])
    for a in range(0, len(p[m - 1])):
        np = g(p[m - 1][a][0])
        for b in range(0, len(np)):
            if np[b] <> "":
                p[m].append((np[b], p[m - 1][a][1] + str(b)))
    for a in range(0, len(p[m])):
        if p[m][a][0] == "~A01":
            fs = p[m][a][1]

# Using the finish sequence (fs), display the steps
for a in range(0, len(fs) + 1):
    for b in range(0, len(p[a])):
        if p[a][b][1] == fs[:a]:
            print(p[a][b][0])

David Vreken - 1 year ago

Log in to reply

Brilliant solution！

Alice Smith - 1 year ago

I just found the shortest path: + to A then go to the first one on the bottom and that goes to the - sign - that gave me the answer Yes.

0 Helpful 0 Interesting 0 Brilliant 1 Confused

Oh, I forget to say that you can't go from one path to another by the intersections. These are actually high-way streets:)

Alice Smith - 1 year ago

Log in to reply

Well, I didn't know at the time...

A Former Brilliant Member - 1 year ago

Log in to reply

Don't worry. You will eventually find the solution:)

Alice Smith - 1 year ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...