Fractal Squares

Algebra Level 2

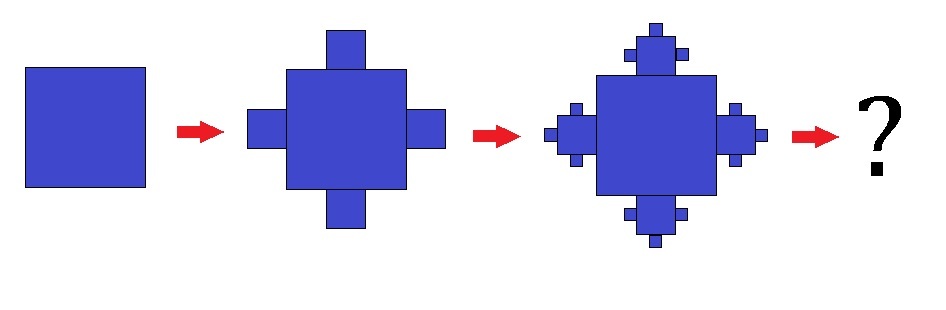
The image above shows a construction of fractal by joining smaller and smaller squares to each side of one single square.

We start with a square of side length 3.
In the second figure, the 4 new squares are formed with a side length of $\dfrac{1}{3}$ of its previous square.
Then from the third figure and so on, the new squares can only be formed on the 3 sides of the previous squares with side length $\dfrac{1}{3}$ of its previous square.

As this recursion continues indefinitely, what does the total area of the figure tend to?

The answer is 15.

2 solutions

Worranat Pakornrat
Mar 4, 2016

$a_{1} = 3\times 3 = 9$

$a_{2} = 3\times 3 + 4\times (1^2) = 13$

$a_{3} = 9 + 4 + 4\times 3\times (\dfrac{1}{3})^2$

$a_{4} = 9 + 4 + 4\times 3\times (\dfrac{1}{3})^2 + 4\times 3^2\times (\dfrac{1}{3^2})^2$

$\vdots$

$a_{n} = 9 + 4 + 4[ (\dfrac{1}{3}) + (\dfrac{1}{9}) + (\dfrac{1}{27}) + \cdots + (\dfrac{1}{3^{n-2}})]$

Let $S = (\dfrac{1}{3}) + (\dfrac{1}{9}) + (\dfrac{1}{27}) + \cdots + (\dfrac{1}{3^{n-2}}) = \dfrac{\dfrac{1}{3}}{1-\dfrac{1}{3}} = \dfrac{1}{2}$ . (This is a sum of a geometric progression)

Hence, $\displaystyle \lim_{n \to \infty} a_{n} = 9 + 4 + 4(\frac{1}{2}) = \boxed{15}$ .

Moderator note:

Great explanation!

One has to be careful because the pattern doesn't happen immediately, and we need to look at $a_3, a_4$ to determine the problem.

Thank you for the review. ;)

Worranat Pakornrat - 5 years, 3 months ago

Scott Rodham
Mar 3, 2017

9 + sum to infinity (a=4 & r = 1/3) giving 15

Fractal Squares

The answer is 15.

2 solutions

Moderator note:

0 pending reports