Fraction Cross Out

Probability Level 3

A student is simplifying fractions, and notices that since 16 64 = 1 4 \frac{16}{64} = \frac{1}{4} , he can “cross out” the sixes as a shortcut.

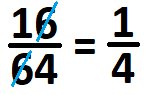
Obviously, this is an incorrect method, but what are all of the fractions that this supposed shortcut works for? Include all fractions a b \frac{a}{b} where a < b a < b , a a has 2 2 unique digits, b b has 2 2 unique digits, and the second digit of a a is the same as the first digit of b b so that they cross out, and enter the sum of all the possible a a and b b values as your answer.


The answer is 432.

David Vreken by David Vreken , 42, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Jeremy Galvagni
Aug 27, 2018

Write the equation as 10 x + y 10 y + z = x z \frac{10x+y}{10y+z}=\frac{x}{z}

Cross multiply and move some terms then refactor to rewrite as 10 x ( y − z ) = z ( y − x ) 10x(y-z)=z(y-x) .

This is significant because there must be a factor of 5 5 on the right which means either z = 5 z=5 or y − x = 5 y-x=5 .

Case 1: z = 5 z=5

The equation becomes 10 x ( y − 5 ) = 5 ( y − x ) 10x(y-5)=5(y-x) . Expand and solve for y y to get y = 9 x 2 x − 1 y=\frac{9x}{2x-1} .

This has three positive integer solutions of which one ( x = y = z = 5 ) x=y=z=5) doesn't count. The good ones are x = 1 , y = 9 x=1, y=9 and x = 2 , y = 6 x=2, y=6 and we have the fractions

19 95 = 1 5 \frac{19}{95}=\frac{1}{5} and 26 65 = 2 5 \frac{26}{65}=\frac{2}{5}

Case 2: y − x = 5 y-x=5

Substituting y = x + 5 y=x+5 the equation becomes 10 x ( x + 5 − z ) = z ( 5 ) 10x(x+5-z)=z(5) . Expand and solve for z z to get z = 2 x 2 + 10 x 2 x + 1 z=\frac{2x^{2}+10x}{2x+1}

This has two positive integer solutions which both work: x = 1 , z = 4 x=1, z=4 and x = 4 , z = 8 x=4, z=8 and we have fractions

16 64 = 1 4 \frac{16}{64}=\frac{1}{4} and 49 98 = 4 8 \frac{49}{98}=\frac{4}{8}

The solution to this problem is then 19 + 95 + 26 + 65 + 16 + 64 + 49 + 98 = 432 19+95+26+65+16+64+49+98=\boxed{432}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Great solution!

David Vreken - 2 years, 9 months ago

Would it be valid to say that 49 98 = 4 8 \frac{49}{98}=\frac{4}{8} is the fully simplified form? If the student is simplifying fractions, then his teacher would mark points off for him not getting the correct answer.

Blan Morrison - 2 years, 8 months ago

Log in to reply

Of course, this is not fully simplified. It's not really simplified at all, but they are equivalent fractions. I couldn't imagine a student reducing 49 to 4 and 98 to 8 as the ratio is not a whole number.

By the wording of the problem, 49 and 98 should be included in the sum.

Jeremy Galvagni - 2 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...