This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Perfect solution...I also have solved this problem using this method...for infinite series this method(supposing the result as x) is very useful.
I just recognized it as phi
same solution :)
Plz illustrate 1st step
Log in to reply
x is the exact same as the one in the second layer because the number of layers between both x s are the same due to the fraction having infinite layers.
for(int i=0;i<10;i++) { x= 1/(1+x); }
cout<<x;
i did it vai programming
The given expression can be written as : 1 + x 1 because , if you remove one element from an infinite set of things, that won't change the infinity much. So here we assume the things after the number 1 in the denominator to be x again(by virtue of above property ).
Rest solution: 1 + x 1 = x 1=(\x^{2}) +x So, \x = 2 − 1 + 5 0 . 5 since\ (\sqrt{5}=2.23) \x = 2 − 1 + 2 . 2 3 \x = 0 . 6 1 8
https://www.xtremepapers.com/community/attachments/sat-work-png.49171/
x = 1/(1+x) x = (sqrt 5 - 1)/2 = 0.618, x = - (sqrt 5 + 1)/2 = -1.618 x = 0.62 or x = -1.62
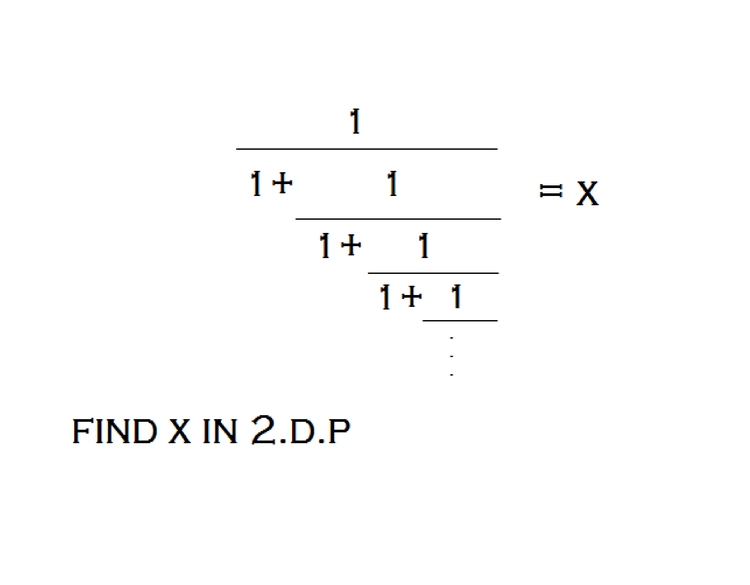
This can be written as 1 + x 1 = x ⟹ x 2 + x − 1 = 0 ⟹ x = 2 − 1 ± 5 .
Clearly x > 0 , so x = 2 5 − 1 = 0 . 6 2 to 2 decimal places.