Fraction of shaded region
What fraction of the decagon is shaded blue?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
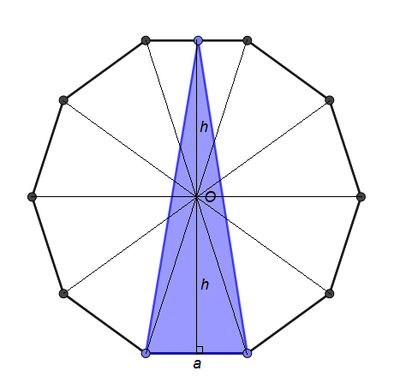 Let the side length and the apothem of the decagon be
a
and
h
respectively. Then the area of the blue triangle
A
blue
=
2
1
a
(
2
h
)
=
a
h
. The area of each of the ten central-angle triangle
A
△
=
2
1
a
h
. The area of the decagon
A
decagon
=
1
0
A
△
=
5
a
h
. The fraction of the decagon is shaded blue
A
decagon
A
blue
=
5
a
h
a
h
=
5
1
.
Let the side length and the apothem of the decagon be
a
and
h
respectively. Then the area of the blue triangle
A
blue
=
2
1
a
(
2
h
)
=
a
h
. The area of each of the ten central-angle triangle
A
△
=
2
1
a
h
. The area of the decagon
A
decagon
=
1
0
A
△
=
5
a
h
. The fraction of the decagon is shaded blue
A
decagon
A
blue
=
5
a
h
a
h
=
5
1
.
If the decagon were divided into 10 congruent triangles, each with one of the 10 sides being its base and the third vertex being the centre of the decagon, then each of these triangles would have 1 0 1 the area of the decagon. The given blue triangle has the same base as one of these triangles but twice the height, and thus has an area 2 × 1 0 1 = 5 1 that of the decagon.