Fractional Integral

Calculus Level 4

$\large \int_0^1 \{ nx \} ^{1/3} \, dx$

The integral above has a closed form when $n$ is a positive integer, find this closed form.

Give your answer to 2 decimal places.

Notation : $\{ \cdot \}$ denotes the fractional part function .

The answer is 0.75.

3 solutions

Aditya Narayan Sharma
May 6, 2016

Put $nx=y$ then,

$\displaystyle I=\frac{1}{n} \int_{0}^{n} \left\{y\right\}^{\frac{1}{3}}dy=\frac{1}{n} \sum_{k=0}^{n-1} \int_{k}^{k+1} (y-k)^{\frac{1}{3}} dy$

Put $\displaystyle y-k=u$ , $\displaystyle I=\frac{1}{n} \sum_{k=0}^{n-1} \int_{0}^{1} u^{\frac{1}{3}} dy$

$I= \frac{3}{4} = 0.75$

展豪張
May 6, 2016

$\displaystyle\int_0^1\{nx\}^{\frac 13}dx$
$\displaystyle=\int_0^{1/n}\{nx\}^{\frac 13}dx+\cdots+\int_{(n-1)/n}^1\{nx\}^{\frac 13}dx$
$\displaystyle=n\int_0^{1/n}(nx)^{\frac 13}dx$ (periodic property)
$\displaystyle=n^{\frac 43}\int_0^{1/n}x^{\frac 13}dx$
$\displaystyle=n^{\frac 43}[\frac 34 x^{\frac 43}]|_0^{1/n}$
$=\dfrac 34$
$=0.75$

Thats great ! Some other solutions are also present but this one is the most fundamental.

Aditya Narayan Sharma - 5 years, 1 month ago

I have a graph in my mind first and I present the solution in this way :)

展豪張 - 5 years, 1 month ago

Ganesh Iyer
May 6, 2016

In the domain [0,1], the value of fractional part of 'nx' is 'nx' itself..

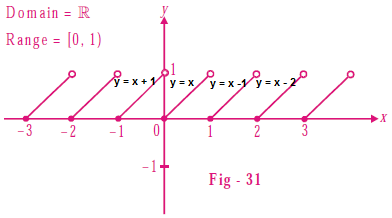
Therefore it is simply an integration of $(nx)^\frac{1}{3}$ from 0 to 1.

Thank you for sharing your approach!

I would like to point out that $\{ nx\}$ is equal to $nx$ in the domain $[0,1)$ only if $n \le 1$ . It is not true for $n > 1$ .
For example, consider $\{3x\}$ . It is equal to $3x$ in the interval $[0, \frac{1}{3})$ , it is $3x-1$ in the interval $[\frac{1}{3}, \frac{2}{3})$ , and $3x-2$ in the interval $[\frac{2}{3}, 1)$ .

Pranshu Gaba - 5 years, 1 month ago

Understood my mistake. :-)

Thankyou for pointing it out. :-)

Ganesh Iyer - 5 years, 1 month ago

Fractional Integral

The answer is 0.75.

3 solutions

0 pending reports