Fractional parts.
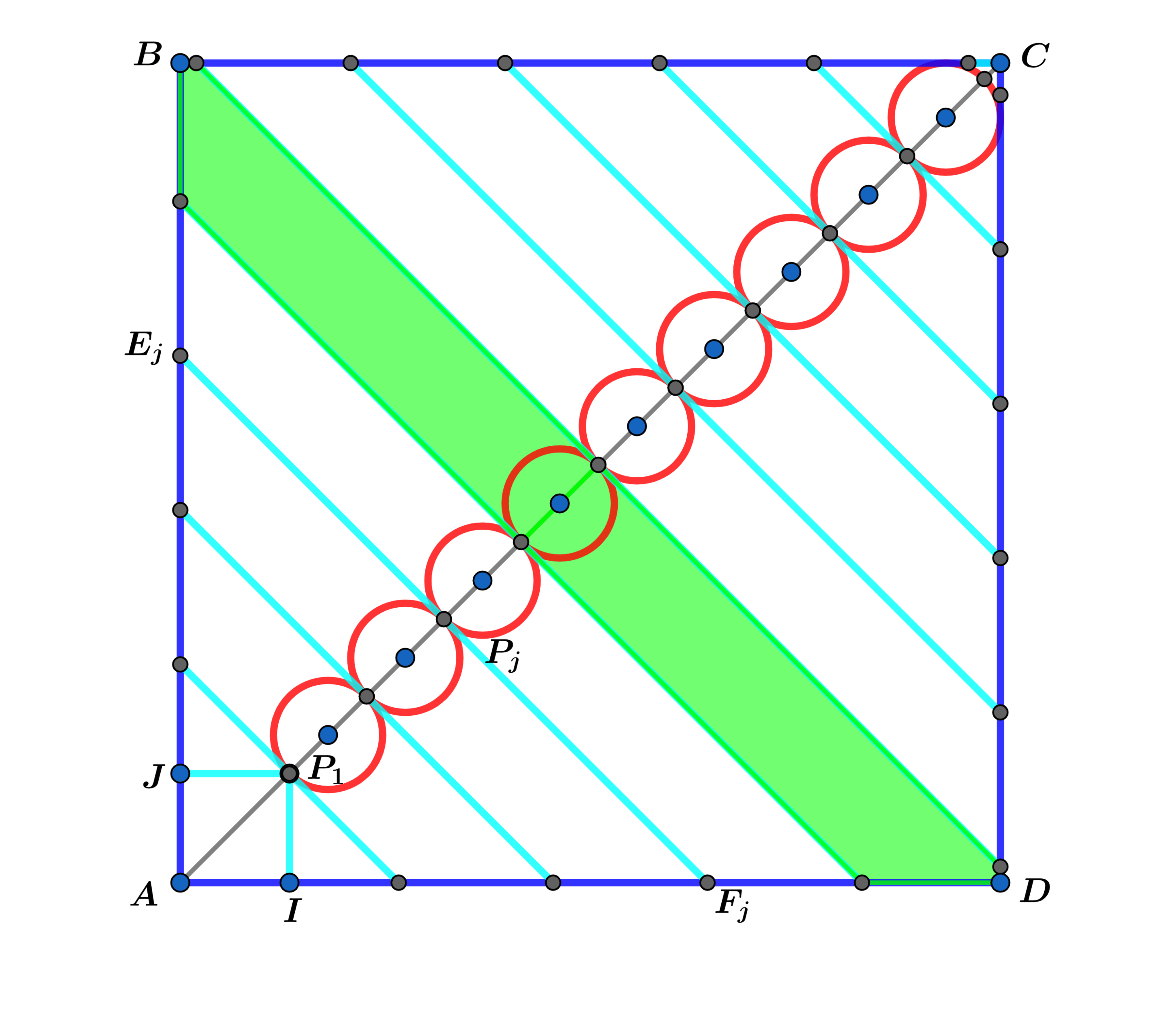
Extend the above diagram to n congruent circles where n is a odd positive integer.
In square A B C D , one of the vertices of square A J P 1 I touches E 1 F 1 at P 1 and E j F j is tangent to circle C j at P j for each integer j , where ( 1 ≤ j ≤ n ) and the radius of each congruent circle is half the side of the square A J P 1 I .
Let A T be the area of the green shaded hexagonal region.
Find the value of n for which A A B C D A T = ( 2 n + 3 2 − 1 ) 2 8 ( 2 − 1 ) { 2 n } − 1 6 ( { 2 n } ) 2 + 4 9 2 1 2 2 − 2 8 1 ,
where { 2 n } represents the fractional part of the number 2 n .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let n be a fixed odd integer, a a side of square A B C D and x a side of square A J P 1 I .
Extending the diagram to n odd congruent circles we obtain:
2 a = 2 x + ( n − 1 ) x + 2 x + 2 x ⟹ 4 a = ( 6 + 2 ( 2 n − 1 ) ) x ⟹
x = 6 + 2 ( 2 n − 1 ) 4 a = 2 ( 3 2 + ( 2 n − 1 ) ) 4 a = 3 2 + ( 2 n − 1 ) 2 2 a
C P ⌊ 2 n ⌋ + 1 = ( n − ( ⌊ 2 n ⌋ + 1 ) + 2 1 + 2 1 ) x =
2 2 ( n − ⌊ 2 n ⌋ ) + 2 − 1 x
Let a n = n − ⌊ 2 n ⌋ ⟹ C P ⌊ 2 n ⌋ + 1 = 3 2 + 2 n − 1 2 ( 2 a n + 2 − 1 ) a
⟹ A △ 1 = ( C P ⌊ 2 n ⌋ + 1 ) 2 = ( 2 n + 3 2 − 1 ) 2 2 ( 2 a n + 2 − 1 ) 2 a 2
A P ⌊ 2 n ⌋ = ( 2 + ( ⌊ 2 n ⌋ − 1 ) ) x = 2 n + 3 2 − 1 2 2 ( ⌊ 2 n ⌋ + 2 − 1 ) a
Let b n = ⌊ 2 n ⌋
⟹ A △ 2 = ( A P b n ) 2 = ( 2 n + 3 2 − 1 ) 2 8 ( b n + 2 − 1 ) 2 a 2
⟹ A △ 1 + A △ 2 = ( 2 n + 3 2 − 1 ) 2 2 ( 4 ( a n 2 + b n 2 ) + 4 ( 2 − 1 ) ( a n + 2 b n ) + 5 ( 3 − 2 ) ) a 2
a n = n − ⌊ 2 n ⌋ = 2 n + { 2 n } and b n = ⌊ 2 n ⌋ = 2 n − { 2 n }
⟹ A △ 1 + A △ 2 = ( 2 n + 3 2 − 1 ) 2 2 ( 2 n 2 + 6 ( 2 − 1 ) n + 5 ( 3 − 2 2 ) + 8 ( { 2 n } ) 2 − 4 { 2 n } a 2
A T = a 2 − ( A △ 1 + A △ 2 )
⟹ A A B C D A T = ( 2 n + 3 2 − 1 ) 2 8 n + 1 4 2 − 1 1 + ( 2 n + 3 2 − 1 ) 2 8 ( 2 − 1 ) { 2 n } − 1 6 ( { 2 n } ) 2
= ( 2 n + 3 2 − 1 ) 2 8 ( 2 − 1 ) { 2 n } − 1 6 ( { 2 n } ) 2 + 4 9 2 1 2 2 − 2 8 1 ⟹
( 2 n + 3 2 − 1 ) 2 8 n + 1 4 2 − 1 1 = 4 9 2 1 2 2 − 2 8 1 ⟹
3 9 2 n + 6 8 6 2 − 5 3 9 = ( 8 4 8 2 − 1 1 2 4 ) n 2 + ( 6 2 1 2 − 4 2 2 0 2 ) n + 5 7 1 4 2 − 7 8 8 3
⟹
( 2 1 2 2 − 2 8 1 ) n 2 + ( 1 4 5 5 − 1 0 5 5 2 ) n + 1 2 5 7 2 − 1 8 3 6 = 0
After simplifying and dropping the negative root we obtain:
n = 2 1 8 5 4 ( 2 1 2 2 + 2 8 1 ) 1 4 7 5 3 9 − 1 0 0 2 5 4 2 + 3 8 4 6 5 − 1 2 0 0 5 2
= 2 1 8 5 4 ( 2 1 2 2 + 2 1 8 ) ( 2 2 3 7 ( 6 9 1 3 2 − 7 3 5 9 ) ) + 3 8 4 6 5 − 1 2 0 0 5 2 =
4 8 7 3 4 4 2 2 6 7 7 1 1 5 2 + 6 0 4 2 6 3 1 + 8 5 7 7 6 9 5 − 2 6 7 7 1 1 5 2 = 4 8 7 3 4 4 2 1 4 6 2 0 3 2 6 = 3 .