A disjointed graph

R.H.S. is integer hence fractional part can be either 0 or 05. In the first case x = 3 and in the second case x = 1.5 ( x = 0 is also a solution.)

$2\langle x \rangle = 3[x]-[x^2]\quad \Rightarrow \langle x \rangle = \dfrac{3[x]-[x^2]}{2}\quad \Rightarrow 0 \le \dfrac{3[x]-[x^2]}{2} <1$ .

If $\quad x<0\quad \Rightarrow \dfrac{3[x]-[x^2]}{2} <0 \ne \langle x \rangle \quad \Rightarrow x \ge 0$ .

From $\quad \dfrac{3[x]-[x^2]}{2} \ge 0 \quad \Rightarrow 3[x]-[x^2] \ge 0 \quad \Rightarrow 3[x] \ge [x^2]\\ \quad \Rightarrow x < \sqrt{10}\quad \Rightarrow 0 \le x < \sqrt{10}$

The surest way to solve the problem is to plot out the graph, as I did with a spreadsheet.

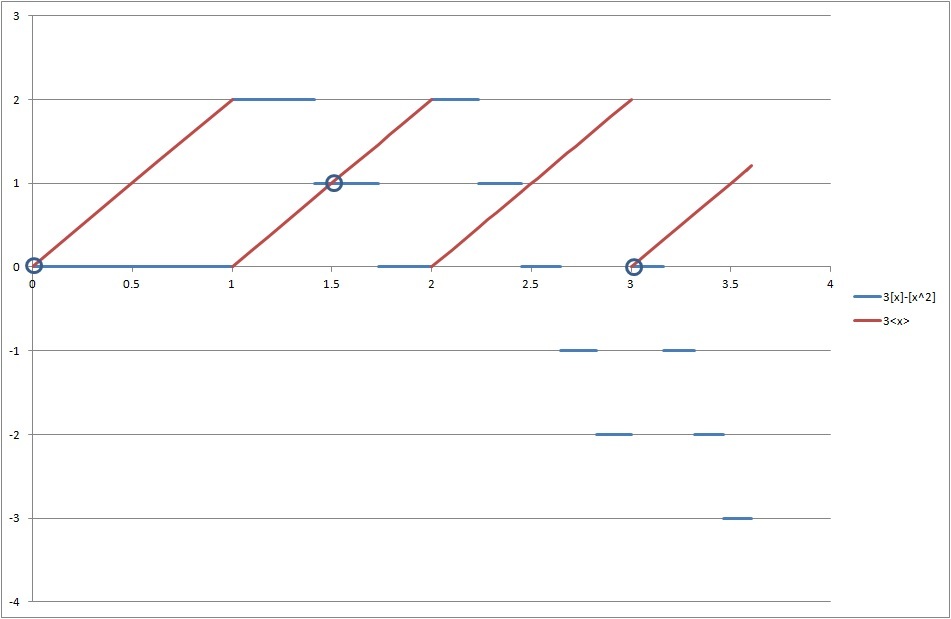
It can be seen there are three solutions:

$\begin{cases} x=0 & \Rightarrow 2\langle 0 \rangle = 3[0]-[0^2] & \Rightarrow 0 \equiv 0 - 0 \\ x=1.5 & \Rightarrow 2\langle 1.5 \rangle = 3[1.5]-[1.5^2] & \Rightarrow 1 \equiv 3 - 2 \\ x= 3 & \Rightarrow 2\langle 3 \rangle = 3[3]-[3^2] & \Rightarrow 0 \equiv 9 - 9 \end{cases}$

Therefore the sum of roots are $\quad 0+1.5+3 = \boxed{4.5}$