Freak with Frequency

Electricity and Magnetism Level 4

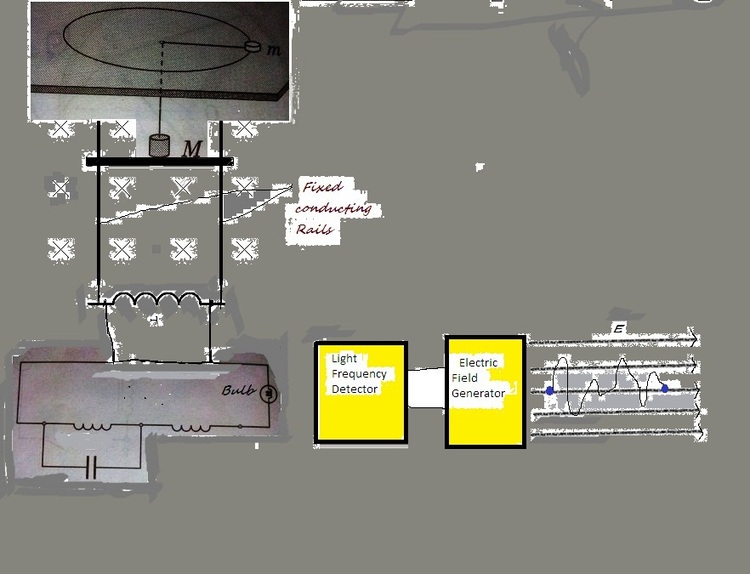In the problem a figure is shown a figure which consist of a mass m=10 kg attached to a string on smooth table whose other end through a very tiny hole in the table is attached to a another mass M=1 kg in the shape of a block attached to a rod of length 1metre.When M is in equilibrium m is rotating on the table with a angular frequency 1radian/sec with a radius r=1metre about the hole. The rod can slide on the a set of vertical smooth parallel conducting rails fixed as shown.There exists a magnetic field B which we can change perpendicular to the plane of the rails. The rails are also attached to a inductor L=1H whose two ends are connected to a circuit given in the figure.The circuit contains another two inductors which are identical but whose inductance is unknown ,a capacitor whose capacitance is unknown and a bulb. In front of the bulb is a Frequency Detector connected to a Electric field generator which generated a uniform electric field E directly proportional to the angular frequency detected by the frequency detector.At time t=0 we release from the same height in the uniform electric field two neutral conducting metal balls. assume that the electric field exists even very below the ball. the metal balls are very small of radius r and mass m and are connected with a very light conducting inextensible thread of length b=2 metres .Initial separation of the balls is a=1meter. Initially M is in equilibrium and m is rotating no current flows anywhere . We displace the (rod and mass)M by a very small distance and release it at t=0 The bulb now is dimmest. the conducting balls attain their maximum horizontal velocity U at some time.

Now we again do this experiment starting from equilibrium by changing the magnetic field so that the bulb is brightest.Now the conducting balls attain a maximum horizontal velocity V at another certain time.Find V-U E = K ω , K = 1 0 12 S I u n i t s E=K\omega,K=10^{12}SIunits Assume r ≪ a r\ll a r = ε π m e t r e s r=\frac{\varepsilon}{\pi}metres

B = 3 0.5 T B=3^{0.5}T at dimmest

the whole experiment setup is carried out at a good distance above the ground.

0 as the frequencies are same whether brightest or dimmest V − U = 3 ∗ ( 2 0.5 − 1 ) ∗ 1 0 12 ε V-U=3*(2^{0.5}-1)*10^{12}\varepsilon V − U = 3 ∗ ( 3 0.5 − 1 ) ∗ 1 0 12 ε V-U=3*(3^{0.5}-1)*10^{12}\varepsilon V − U = 7 ∗ ( 3 0.5 − 1 ) ∗ 1 0 12 ε V-U=7*(3^{0.5}-1)*10^{12}\varepsilon

Milun Moghe by Milun Moghe , 25, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Milun Moghe
Feb 16, 2014

It is clear that when we displace the mass M a bit two forces restore it .One due to the changing radius centripetal acceleration and thus ω \omega changes to say ω 1 \omega_{1}

m ω 1 2 ( r − x ) − m ω 2 r = ( m + M ) a 1 m\omega_{1}^{2}(r-x)-m\omega^{2}r=(m+M)a_{1}

conservation of angular momentum gives

( r − x ) ω 1 = r ω (r-x)\omega_{1}=r\omega

the restoring force due to the inductor or change in flux in the circuit can be clearly given by B 2 l 2 x L = ( m + M ) a 2 \frac{B^{2}l^{2}x}{L}=(m+M)a_{2}

As here both the change in flux as well as the change in radius is restoring

therefore the equation of SHM can be given by. ( M + m ) ( a 1 + a 2 ) = ( B 2 l 2 L + 3 m ω 2 ) x = ω 2 2 x (M+m)(a_{1}+a_{2})=(\frac{B^{2}l^{2}}{L}+3m\omega^{2})x=\omega_{2}^{2}x

The system above the inductor will serve as an ac source for the below circuit .The potential difference across the inductor has a frequency ω 2 = a \omega_{2}=a

Now let us consider the circuit here L and C as the inductance though it doesn't matter what we take.

we can find the net impedance using complex no

Z = R − i L a + i ( − i a L ) a C I a c − i a L Z=R-iLa+\frac{\frac{i(-iaL)}{aC}}{\frac{I}{ac}-iaL}

when Z is minimum bulb is brightest as P o w e r = V 2 Z Power=\frac{V^{2}}{Z} and vice versa

let min brightness be at a = a 1 a=a_{1} and maximum at a = a 2 a=a_{2}

here V is constant due to SHM and not damped SHM

we get a 1 2 = 1 L C a_{1}^{2}=\frac{1}{LC} and a 2 2 = 2 L C a_{2}^{2}=\frac{2}{LC}

therefore a 2 = 2 0.5 a 1 a_{2}=2^{0.5}a_{1}

Given that the Electric Field is E

As we have to deal with horizontal max vel lets for the time being forget about gravity.

I chose a coordinate system with the origin at the centre of mass of the two spheres.Because the sphere are small compared to the other dimensions in the problem they can be treated as point charges (except when the sphere change position, charge moves from one to the other through the connecting wire). But, for macroscopic objects (even very small ones), the changes in the positions are sluggish enough that the current in the wire will be very small and I will approximate it to 0.The system is approximately in electrostatic equillibrium at all times.

If I let Q represent the charge that moves from sphere to the other, then the potential difference due to the charges on the sphere is △ V = 2 k Q r \triangle V=\frac{2kQ}{r}

The potential difference due to the charge separation just balences the potential difference that creates the external electric field. 2 E x = 2 k Q r 2Ex=\frac{2kQ}{r}

There is a force of attraction given by

F a t t = k Q 2 x 2 = k E 2 r 2 x 2 k 2 r 2 = E 2 r 2 k = c o n s t a n t F_{att}=\frac{kQ^{2}}{x^{2}}=\frac{kE^{2}r^{2}x^{2}}{k^{2}r^{2}}=\frac{E^{2}r^{2}}{k}=constant

There is also a force due to external field

F E = E q = E 2 r x k F_{E}=Eq=\frac{E^{2}rx}{k}

F n e t = E 2 r x k − E 2 r 2 k F_{net}=\frac{E^{2}rx}{k}-\frac{E^{2}r^{2}}{k}

The velocity can only increase until length is full taut. From the coservation of Energy the kinetic energy of the sphere is equal to the work done by the net force that accelerates it

m v 2 2 = ∫ a 2 b 2 F n e t d x \frac{mv^{2}}{2}=\int_{\frac{a}{2}}^{\frac{b}{2}}F_{net}dx

we get v = E r m k ( ( b 2 − a 2 ) 4 − r ( b − a ) ) v=E\sqrt{\frac{r}{mk}(\frac{(b^{2}-a^{2})}{4}-r(b-a))}

taking the approximation r ≪ a + b 4 r\ll\frac{a+b}{4}

we get v = E r m k ( ( b 2 − a 2 ) 4 ) v=E\sqrt{\frac{r}{mk}(\frac{(b^{2}-a^{2})}{4})}

so we can get the maximum horizontal velocities in both cases. when dimmest as well as when brightest and finally we can find out (V-U).

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Freaky isn't it?

Milun Moghe - 7 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...