Free electron in magnetic field (with a spark of quantum theory)

Electricity and Magnetism Level 4

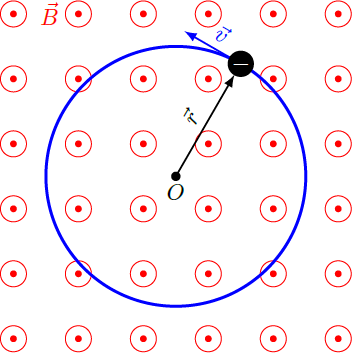
A free electron with mass m m and charge q = − e q = -e , which moves in the xy-plane, is forced by a homogeneous magnetic field B ⃗ \vec B in the z-direction on a circular path with radius r r . This phenomenon can be demonstrated in a classroom experiment using an electron tube (Teltron tube), in which the electrons stimulate gas molecules through collisions and make them glow. At a magnetic field of 1.3 millitesla, the circular tracer of the electrons in this experiment has a typical radius of a few centimeters. How big is the smallest possible orbital radius r r for electrons in the same magnetic field B = 1.3 mT B = 1.3 \,\text{mT} according to the quantum theory?

Hints: According to the Bohr-Sommerfeld quantization condition, only those circular orbits are permitted for the electron for which the orbital angular momentum L L is just a half-integer multiple of the reduced Planck's constant ℏ \hbar : L = m v r = ℏ ( n + 1 2 ) , n = 0 , 1 , 2 , 3 , … L = m v r = \hbar \left( n + \frac{1}{2} \right), \quad n = 0,1,2,3,\dots The relevant physical constants are e ≈ 1.6 ⋅ 1 0 − 19 C m ≈ 9.1 ⋅ 1 0 − 31 kg ℏ ≈ 1.05 ⋅ 1 0 − 34 J s \begin{aligned} e &\approx 1.6 \cdot 10^{-19}\, \text{C} \\ m &\approx 9.1 \cdot 10^{-31} \, \text{kg} \\ \hbar &\approx 1.05 \cdot 10^{-34} \,\text{J}\,\text{s} \end{aligned}

This is just a Semiclassical approach that does not fully describe the physical behavior of the electron. However, the quantization condition gives us classical orbits that correspond to different quantum mechanical states and describe the mean value of the radial distance r r .

half a micrometer half a femtometer half a picometer half a millimeter half a nanometer

Markus Michelmann by Markus Michelmann , 35, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

According to classical Newtons laws, the electron orbit results from the balance of lorentz force F ⃗ L \vec F_L and centrifugal force F ⃗ cf \vec F_\text{cf} : F ⃗ L = ( − e ) ⋅ v ⃗ × B ⃗ = − F ⃗ cf = − m v 2 r e ⃗ r ⇒ e v B = m v 2 r ⇒ v = e m B r \begin{aligned} \vec F_L = (-e) \cdot \vec v \times \vec B &= -\vec F_\text{cf} = -m \frac{v^2}{r} \vec e_r \\ \Rightarrow \quad e v B &= m \frac{v^2}{r}\\ \Rightarrow \quad v &= \frac{e}{m} B r \end{aligned} If we use this result and insert it into the quantization condition, we obtain discrete values r n r_n for the orbit radius: L = m v r = e B r 2 = ℏ ( n + 1 2 ) ⇒ r n = ℏ e B ( n + 1 2 ) \begin{aligned} L = m v r = e B r^2 &= \hbar \left(n + \frac{1}{2} \right) \\ \Rightarrow \quad r_n &= \sqrt{\frac{\hbar}{e B} \left( n + \frac{1}{2} \right) } \end{aligned} The smallest radius for the case n = 0 n = 0 yields r 0 = ℏ 2 e B = 5.03 ⋅ 1 0 − 7 m ≈ 0.5 μ m r_0 = \sqrt{\frac{\hbar}{2e B} } = 5.03 \cdot 10^{-7} \,\text{m} \approx 0.5 \, \mu \text{m}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...