Free Test
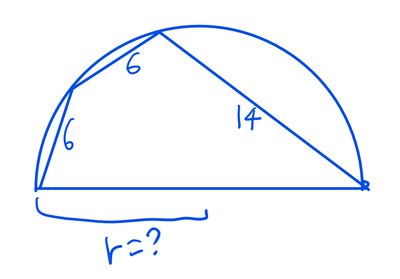
As shown in the figure, an irregular quadrilateral is inscribed in a semicircle with its base being the diameter of the semicircle. Find the radius r of the semicircle.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
i did it differently but it is the same answer
Let the center of the circle be O and the four vertices of the given quadrilateral be A , B , C , D respectively with A D as diameter. Let the angle ∠ A O B be α . Then ∠ C O D is π − 2 α . Using Cosine Rules to the triangles △ A O B and △ C O D we get cos α = 1 − r 2 1 8 = r 7 , where r is the radius of the circle. Solving we get r = 9
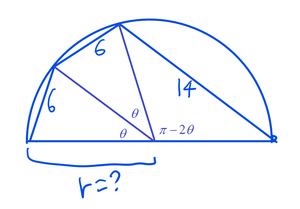
Let the angle extended at the center of the semicircle by the side of quadrilateral with length 6 be θ . By cosine rule we have:
{ r 2 + r 2 − 2 r 2 cos θ = 6 2 r 2 + r 2 − 2 r 2 cos ( π − 2 θ ) ) = 1 4 2 ⟹ r 2 ( 1 − cos θ ) = 1 8 ⟹ r 2 ( 1 − cos ( π − 2 θ ) = 9 8 . . . ( 1 ) . . . ( 2 )
( 2 ) ( 1 ) : 1 − cos ( π − 2 θ ) 1 − cos θ 1 + cos 2 θ 1 − cos θ 2 cos 2 θ 1 − cos θ 1 8 cos 2 θ + 4 9 cos θ − 4 9 ( 9 cos θ − 7 ) ( 2 cos θ + 7 ) ⟹ cos θ = 4 9 9 = 4 9 9 = 4 9 9 = 0 = 0 = 9 7 Note that cos ( π − ϕ ) = − cos ϕ and cos 2 ϕ = 2 cos 2 ϕ − 1 Rearrange Since cos θ > 0
From ( 1 ) : r 2 ( 1 − 9 7 ) = 1 8 ⟹ r = 9 .
chew seong the easy why to do it is like this
by this equation
cos2x=14/2r sinx=6/2r
so you solve for r and you get 9 and -2 but you pick the 9
Log in to reply
Because r is the radius it cannot be negative.
We are given that A C = C D = 6 and B D = 1 4 , and we infer from the semicircle that A O = B O = C O = D O = r .
Let F be the midpoint of BD. Then, since △ B O D is isosceles, ∠ O F D is right. Similarly, E is the midpoint of AD by symmetry and △ A O D is isosceles, so ∠ O E D is right. Thirdly, ∠ A D B is right, since it is subtended by the diameter of a circle.
Hence, O F D E is a rectangle, which implies E O = D F = 2 1 4 = 7 .
Now, consider the right triangle △ O D E . By the Pythagorean theorem, E D 2 + E O 2 ⟹ E D 2 + 7 2 ⟹ E D 2 = D O 2 = r 2 = r 2 − 7 2 Now consider the right triangle △ C D E . Notice that C E = C O − E O = r − 7 . By the Pythagorean theorem again, E D 2 + C E 2 ⟹ r 2 − 7 2 + ( r − 7 ) 2 ⟹ r 2 − 4 9 + r 2 − 1 4 r + 4 9 ⟹ 2 r 2 − 1 4 r − 3 6 ⟹ 2 ( r − 9 ) ( r + 2 ) ⟹ r = 9 = C D 2 = 6 2 = 3 6 = 0 = 0 , r = − 2 Since r cannot be negative, the solution is r = 9 .