Frequency response 3
Consider the circuit on the image with a voltage source V = 1 0 2 sin ( ω t ) . What is the effective voltage across the capacitor as the frequency of the voltage source goes to zero?
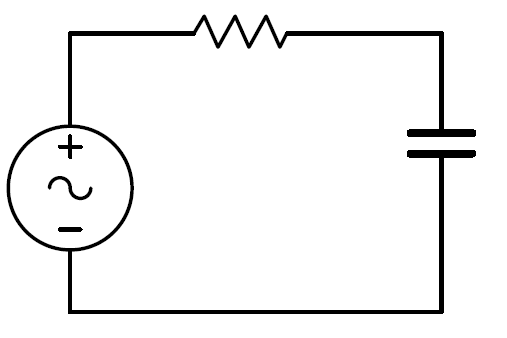
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The resistor with the capacitor are a voltage divider. Let's call Z c the capacitor's impedance and R the resistor's impedance, we can calculate the voltage across the capacitor as
V o = V i ⋅ ( R + Z c Z c )
We can calculate Z c in function of the frequency as Z c = 2 π f C − j with j = − 1 . It's easy to see that the capacitor's impedance will go to infinity as the frequency goes to zero, which means that
lim Z c → 0 ( R + Z c Z c ) = lim Z c → 0 ( 1 + Z c R 1 ) = 1 so V o = V i
Since the voltages will be equal, the voltage effective voltage across the capacitor will be equal to the effective voltage of the power source, which is 2 V p = 2 1 0 2 = 1 0 V
When ω → 0 , the voltage source becomes a DC (direct-current) source. Then the capacitor will take on the voltage of the voltage source when fully charged that is 1 0 V .