Friction +Differential Torque+Time = No motion
A square plate of side a having surface mass density σ is placed on a rough surface. Initially angular velocity ω 0 about axis perpendicular to plane and passing through center of mass is given then plate takes time t to come to rest. If we provide same ω 0 about axis perpendicular to plane and passing through one of the corner then plate takes time N t to come to rest. Find out the value of N .
Coefficient of Kinetic Friction is η .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Did the same!! A qualitative analysis gives the answer very fast! :p
We can use scaling arguments to compare the torque on the two squares.
Divide the first square into 4 small squares having sides
2
ℓ
and meeting at center.
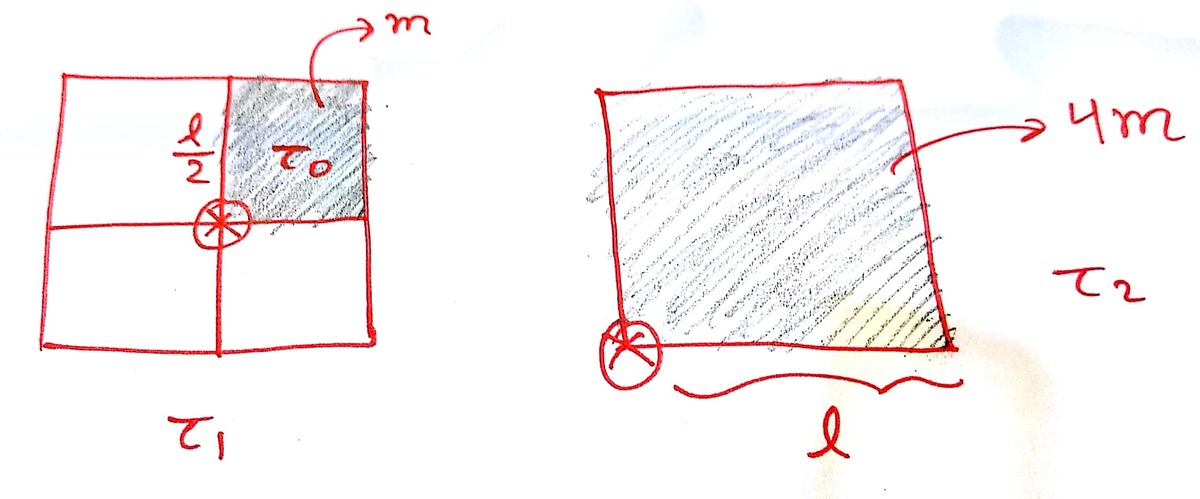
Since the total torque about identical configuration (the corners in this case) for a small square and a larger one will scale in proportion to its mass and length, ( τ = ∫ μ g r d m ) so τ 2 = m 4 m ℓ / 2 ℓ τ 0 and also τ 1 = 4 τ 0 .
Now as for the moment of inertia it varies in proportion with m r 2 (we can use the nice symmetries of regular objects in using scaling arguments for I ) and thus I 2 = 2 2 2 2 I 0 = 4 I 1 .
Using τ axis = I axis α , we get α 2 = 2 α 1 .
The time taken to stop t = α Δ ω is t 2 = 2 t 1 .
Nishant Rai plz post a solution
I see you have solved the problem, please share how you attempted and solved the question. I am a it busy right now, exams are coming, will surely post the solution after 30th may.
Log in to reply
nope i didnt solve this, it was a lucky guess, because u dont find integral coefficient of friction too large
Plz note i will treat ...
mass distribution by '§"
coefficient of friction by 'ń"
angular velocity by 'W"
edge length 'a"
time by "t"
For the case when axis of rotation passes through centre of mass
TORQUE= ń§g(a^3)/4= §(a^4) W/3t.......1
For the case when axis of rotation passes through edge
TORQUE=ń§g(a^3) /2 = §(a^4) W/ 3Nt .......2
On equating above two equations we will get
N= 2
The square spinning about the center can be viewed as four smaller squares (half the size) spinning about the corner. To every surface element d x d y at distance r from the axis on the second square belongs therefore a surface element d x d y at distance 2 1 r on the first square.
The torque on each square is the integral of η σ g r over the surface. Therefore the torque on the second square is twice as much as on the first square.
The rotational inertia is the surface integral of σ r 2 . Therefore the rotational inertia of the second square is four times larger than that of the first square.
The rotational acceleration α = τ / I of the second square is therefore 4 / 2 = 2 1 of that of the first square.
Finally, since t = ω 0 / α , the time needed to slow the second square is twice as much as for the first square.