Friction in collision
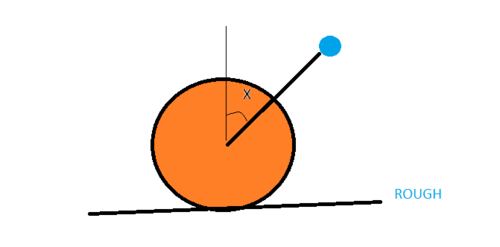A large sphere rests on a rough horizontal ground,
A ball of mass 'm' is thrown towards it along one of its radius at a speed 'u' , along an angle 'x' with the vertical
Find the angle with the vertical at which the ball should strike (find x) so that the large sphere pure rolls immediately after collision.
if the answer can be expressed as arctan(x) then find x.
Collision need not be necessarily elastic
Details:
coefficient of friction=1
mass of large sphere = 1
radius of large sphere = sqroot(0.4)
Note:
1)consider the coefficient of friction to be constant during the instant of collision which is not true but assume for this question
2)Treat ground as immovable infinitely heavy object as usual
The answer is 3.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
i have put the last inequality sign wrong in a hurry !
the collision need not be elastic necessarily which invalidates your working although your answer is correct
simply use kN=f and now integrate both sides with respect to time to realise the fact that the impulse due to friction is k times the impulse due to normal reaction of ground,, now since the sphere is constrained to move horizontally, so the ground provides equal and opposite impulse upward,, thus whatever impulse the sphere recieves say J, the component normal to ground is jcos(x) and thus frictional impulse is k J cos(x) ,
now proceed.
@Mvs Saketh
Error in the question t a n ( 3 7 0 ) = 4 3
It is only that t a n ( 3 7 0 ) ≈ 4 3
@Mvs Saketh @Ronak agarwal
Can anyone Post full solution for this Question Please ??
But there will also be an impulse J sin(x)( component of J in the horizontal direction) which you have not taken into account. Why? If I take that into account, then I am getting 8.5 as answer, which should be the actual answer, right or wrong?
Log in to reply
I too got 8.5
image
If the sphere does not bounce then
J n = J c o s ( x ) ..........(1)
Let v be the velocity of the com of the sphere after collision so
J s i n x − J c o s x = m v (value of μ is 1)...........(3)
Angular impulse will only be provided by the friction force.
So J c o s ( x ) R = I C o M ω ...............(4)
As the sphere rolls after collision so v = R ω
On solving I got θ = a r c t a n ( 3 . 4 9 . Is this correct?
Also if there is some impulse due to friction the ball will surely roll, you can't neglect the fact that the angular impulse due to all the normal forces and the gravity will be 0, and it is well known that angular impulse due to friciton is non zero, hence it will roll.
At the end it is impossible for the sphere not to roll if the friction is sufficient. Kindly please check the question again.
Log in to reply
U are correct.... the frictional impulse can cause rotation and immediately after that it will oppose the relative motion at surface thus creating a non 0 net force causing it to move or roll... didnt see that.. i have modified the question accordingly,,, thanks :)
The ball may roll for a range of angle. That angle for which friction is limiting should have been asked
Log in to reply
No I said pure roll immediately after collision and not any time after collision.... also pure roll and not just roll... hence only a particular angle is there
answer should be 8.5
Awesome Question!
Initially it looks like there is no information available at all or some information is missing but at the end of the day,we only need co-efficient of friction!
ur ques are very appropriate for inpho.
Why is there so fuss about it ? here is a full solution , some guys were asking !