Friction, you make my head right round!
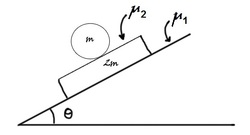 A sphere of mass
and radius
is placed on a rough plank of mass
. This system is placed on a rough inclined plane, with an incline of
.
A sphere of mass
and radius
is placed on a rough plank of mass
. This system is placed on a rough inclined plane, with an incline of
.
The friction coefficient between the plank and the incline is , and that between sphere and plank is .
Find the maximum value of , such that the sphere is always pure rolling on the plank.
Details and Assumptions:
The answer is 2.66667.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First of all this problem is not incorrect nor is it poorly stated.
Second,we do not need the values of mass and radius.
Now,considering the limiting case :
1 . On the sphere there will be two forces : m g s i n θ <left> and μ 2 m g c o s θ <right>
2 . On the plank there will be three forces : μ 2 m g c o s θ <left> , 2 m g s i n θ <left> and μ 1 3 m g c o s θ <right>
3 . Apply Newton's Second Law and you should get the following equations : a s p h e r e / e a r t h = g s i n θ − μ 2 g c o s θ
a p l a n k / e a r t h = 2 g ( c o s θ ( μ 2 − 3 μ 1 ) + 2 s i n θ )
From torque relation , τ = I α < pure rolling,limiting case> a = r α >: we get a s p h e r e / p l a n k = 2 5 μ 2 g c o s θ
Now, a s p h e r e / p l a n k = a s p h e r e / e a r t h − a p l a n k / e a r t h
Equating, we get μ 2 μ 1 = 3 8 .