Frictional oscillations -2
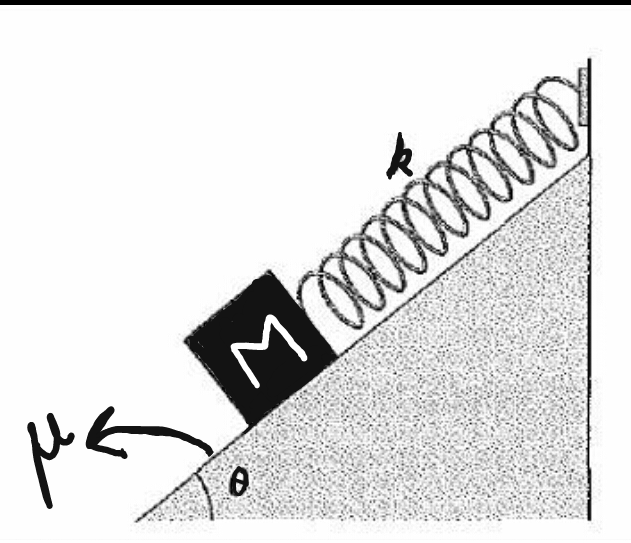 A block of mass M kg is placed of a fixed rough incline of inclination
and coefficient of friction
connected to a spring of spring constant k N/m. Initially the spring is in relaxed state . Then the block is left to move.
A block of mass M kg is placed of a fixed rough incline of inclination
and coefficient of friction
connected to a spring of spring constant k N/m. Initially the spring is in relaxed state . Then the block is left to move.
Let denote the increment of length of spring when it comes to rest time.
Find are integers.
Take .
ORIGINAL
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The forces on the block in the x -direction are a component of its weight M g sin θ , the spring force − k x , and friction ± m g μ cos θ . Notice that the net work done on the block from x n to x n + 1 is 0 because there is no net change in the block's velocity, so ∫ x n x n + 1 ( M g sin θ ± M g μ cos θ − k x ) d x = 0 . When we solve this integral equation for x n + 1 , we obtain the recurrence relation x n + 1 = − x n + k 2 M g ( sin θ ± μ cos θ ) . The sign of μ cos θ alternates. When n = 0 , friction and gravity are working against each other so μ cos θ is negative. In general, we can write x n + 1 = − x n + k 2 M g [ sin θ + ( − 1 ) n + 1 μ cos θ ] . In terms of a , b , c , and d , this recurrence relation is k M g ( − 1 ) n + 1 [ a ( b n + 1 − c ) sin θ + d μ ( n + 1 ) cos θ ] = − k M g ( − 1 ) n [ a ( b n − c ) sin θ + d μ n cos θ ] + k 2 M g [ sin θ + ( − 1 ) n + 1 μ cos θ ] . When we gather the sin θ terms on the right and equate the coefficients of sin θ on the left and right, we obtain k M g ( − 1 ) n + 1 a ( b n + 1 − c ) = k M g ( − 1 ) n [ 2 ( − 1 ) n − a ( b n − c ) ] , which simplifies to − a b n ( b − 1 ) = 2 ( − 1 ) n . This equation holds for all n only if b = − 1 ⟹ − a ( − 1 ) n ( − 1 − 1 ) = 2 ( − 1 ) n ⟹ a = 1 . When we equate the coefficients of cos θ from the two sides of the recurrence, we obtain k M g ( − 1 ) n + 1 d μ ( n + 1 ) = k M g ( − 1 ) n + 1 ( 2 μ + d μ n ) , which simplifies to d ( n + 1 ) = 2 + d n ⟹ d = 2 . Now we have found that a = 1 , b = − 1 , and d = 2 . To find c , recall that the block is released from rest when the spring is at its natural length, so 0 = x 0 = k M g ( − 1 ) 0 ( 1 [ ( − 1 ) 0 − c ] sin θ + 2 μ ( 0 ) cos θ ) = k M g ( 1 − c ) sin θ . The first and last parts of this equation imply k M g ( 1 − c ) sin θ = 0 ⟹ c = 1 . Therefore, we have found a = c = 1 , b = − 1 , d = 2 , and a 2 + b 2 + c 2 + d 2 + a + b + c + d = 1 0 .