Frictional oscillations-1
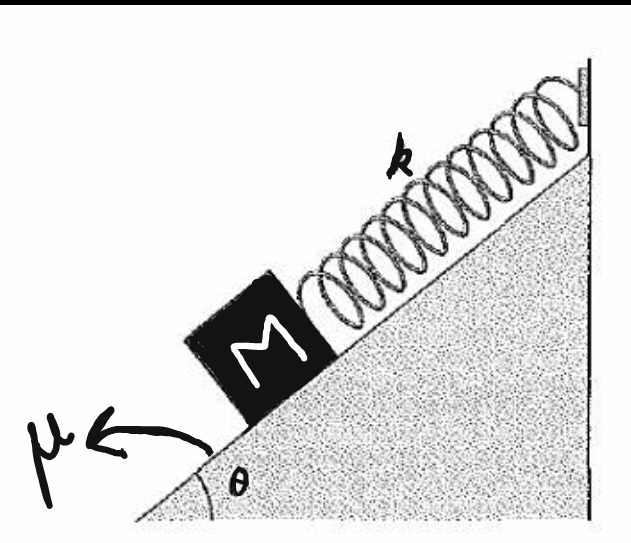 A block of mass M = 2 kg is placed of a fixed rough incline of inclination
and coefficient of friction
connected to a spring of spring constant 100 N/m.
Initially the spring is in relaxed state with length = 10 cm. Then the block is left to move.
A block of mass M = 2 kg is placed of a fixed rough incline of inclination
and coefficient of friction
connected to a spring of spring constant 100 N/m.
Initially the spring is in relaxed state with length = 10 cm. Then the block is left to move.
A= Increment in the length (in cms) in spring when block is completely at rest.
B= Total distance (in cms) travelled by the block before coming to complete rest.
C= No. of times it comes to momentary rest(including the absolute rest)
Find A+B+C=?
Take .
ORIGINAL
The answer is 119.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Because the acceleration of the block is in the plane of the slope, we deduce that the normal force has to be constant , and is given by F n = m g cos θ
The forces that determine the motion are along the slope of the plane:
For a moment, if we ignore friction, we see that gravitation is canceled out by spring force at x = − 1 4 cm . Setting our origin at -14cm below where the block starts, this compensates for the parallel force, and using the values k = 1 , m = 2 , g = 1 0 , sin θ = 1 0 7 , cos θ = 1 − 1 0 0 4 9 = 1 0 0 5 1 we now get the differential equations
2 x ¨ = 1 − x when moving downward
2 x ¨ = − 1 − x when moving upward
For the first stroke, using the starting conditions x ( 0 ) = 1 4 and x ˙ ( 0 ) = 0 we get x ( t ) = 1 + 1 3 cos 2 t
This ends when x ˙ ( t ) = 2 1 3 sin 2 t = 0 , so at t 1 = 2 π .
Hence we have x ( t 1 ) = 1 − 1 3 = − 1 2
Using the second d.e. and conditions x ( t 1 ) = − 1 2 , x ˙ ( t 1 ) = 0 we get
x ( t ) = 1 + 1 3 cos 2 t for t ∈ [ 0 , 2 π ]
x ( t ) = − 1 + 1 1 cos 2 t for t ∈ [ 2 π , 2 2 π ]
x ( t ) = 1 + 9 cos 2 t for t ∈ [ 2 2 π , 3 2 π ]
x ( t ) = − 1 + 7 cos 2 t for t ∈ [ 3 2 π , 4 2 π ]
x ( t ) = 1 + 5 cos 2 t for t ∈ [ 4 2 π , 5 2 π ]
x ( t ) = − 1 + 3 cos 2 t for t ∈ [ 5 2 π , 6 2 π ]
x ( t ) = 1 + cos 2 t for t ∈ [ 6 2 π , 7 2 π ]
Now motion will stop when the block halts at a distance from equilibrium small enough that friction can hold the spring force. Since the friction = ∣ F f ∣ ≤ μ m g cos θ = 1 , this maximum distance from equilibrium is 1. So the block stops at -12, +10, -8, +6, -4, +2, and finally at 0.
A. We already saw that the spring was stretched by 14 cm.
B. Total distance traveled=14+12+12+10+10+8+8+6+6+4+4+2 = 98 cm. Energy check using this result: Work done =1×0.98=0.98J; Spring energy =0.5×100×(0.14)^2=0.98 J
C. We count 7 stops.
So the required answer is 1 4 + 9 8 + 7 = 1 1 9 .