Frictional Track
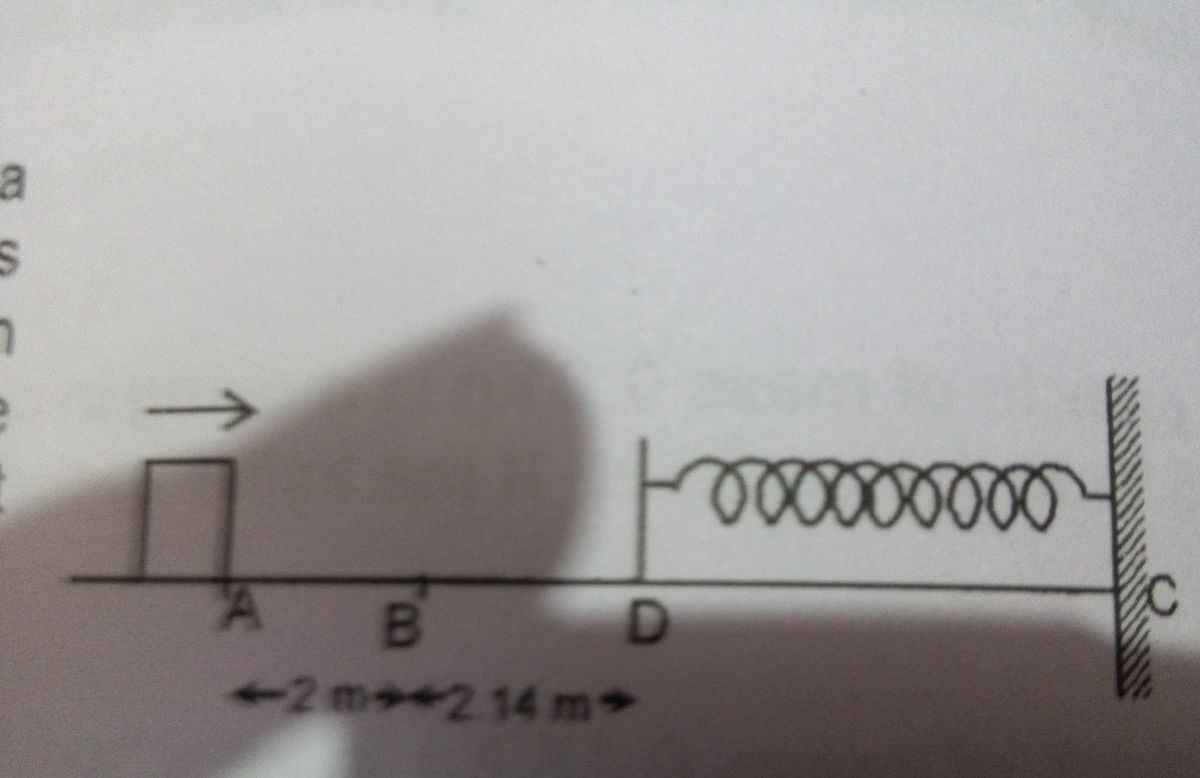
0.5 kg block slides from the points A on a horizontal track with an initial speed of 3 m/s towards a weightless horizontal spring of length 1 m and force constant of 2 N/m. The part AB of the track is frictionless and the part BC has coefficient of static and kinetic friction as 0.22 and 0. 2 respectively. Find the total distance through which the block movez before it comes to rest. Length of AB is 2 m and that of BD is 2.14 m.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The block moves without losing any speed on AB. On BD the block faces kinetic friction of magnitude Fk=(0.2)(0.5)(9.8)N=0.98N So,it delelerates at =(0.98÷0.5)m/s^2 = 1.96 m/s^2 At point d, the speed of the block is v=sqrt(3^2 - 2(1.96)(2.14))m/s=0.782 m/s
At that point, the kinetic energy is, Ek=(0.5)(0.5)(0.782)^2 J = 0.1528 J
If the block momenterily stops at a distance 'x' from point D, then- 0.5kx^2 + 0.2*mgx= 0.1528 [conservation of energy] solving the equation gives x=0.14 m
At that time spring force Fs=0.14k=0.28 N But static frictional force Ff=(0.22mg)= 1.078N Ff>Fs ; So the block totally stops there...
The total distance is = (2+2.14+0.14)m =4.28 m = 4.2 m (almost)