Friendly Quadritics
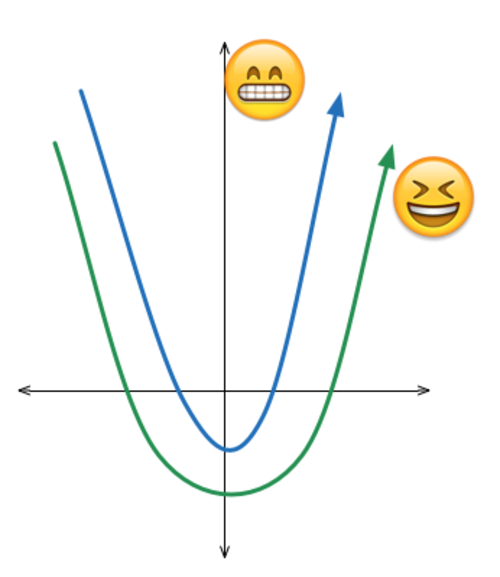Quadratic (A) is a
friend
of quadratic (B) if both the roots of (A) lie between the roots of (B).
Then find the number of integral values of a for which x 2 − 1 0 0 x + a 2 = 0 is a friend of x 2 − 1 0 0 x + 2 a 2 − 1 4 a + 3 3 = 0 .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Can u please recheck ur soln.
Log in to reply
Yes you are right as close the roots get the more is their product so Product of roots of A is greater than Product of roots of B.
To be a friend, the graph of A has to lie completely above B i.e A > B
x 2 − 1 0 0 x + a 2 > x 2 − 1 0 0 x + 2 a 2 − 1 4 a + 3 3 a 2 − 1 4 a + 3 3 < 0 ( a − 1 1 ) ( a − 3 ) < 0 ∴ a ∈ ( ( 3 , 1 1 ) ∴ a ∈ 4 , 5 , 6 , 7 , 8 , 9 , 1 0
Notice that by translating f ( x ) upwards, we obtain g ( x ) which will have roots between that of f ( x ) , hence a friend of f ( x ) , similar to what the picture has shown.
We therefore need a 2 − 1 4 a + 3 3 < 0
( a − 3 ) ( a − 1 1 ) < 0
Since a takes on integral values, a = 4 , 5 , 6 , 7 , 8 , 9 or 1 0 , which gives us 7 solutions.