A Froggy Game of Logic
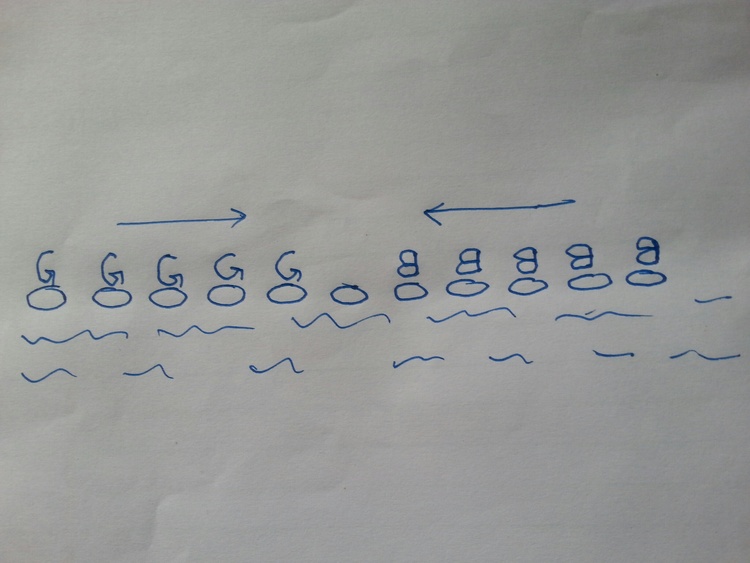 There are 5 green frogs on the left side of the swamp and 5 blue frogs on the right side of the swamp. They are sitting on rocks. The central rock is empty.
There are 5 green frogs on the left side of the swamp and 5 blue frogs on the right side of the swamp. They are sitting on rocks. The central rock is empty.
Your task is to swap their places. i.e.: at the end the 5 blue frogs should be on the left, the 5 green frogs should be on the right and the central rock should be free.
Each frog can only move forward. The direction of travel is shown by the respective arrows.
A frog can advance by one step, if the space in front of it is free.
A frog can jump over another, only if the other frog is of the other color. You can jump over only one frog of other color at a time into the vacant space immediately behind it.
How many moves would it take for the green and blue frogs to swap places?
Can you generalize for frogs on either side?
This problem is inspired by a game I watched my kids play.
The answer is 35.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The key idea here is, that you never want to be in a position where two frogs of the same color are next to each other.
As the frogs have to alternate with each other and jump over each other, that makes n ∗ n = n 2 jumps. The n + n = 2 n are the non-jump slides that the frogs move.
The generalization is that for n frogs on either side it will take n 2 + 2 n or ( n + 1 ) 2 − 1 moves.