Frog is jumping infinitively - hard
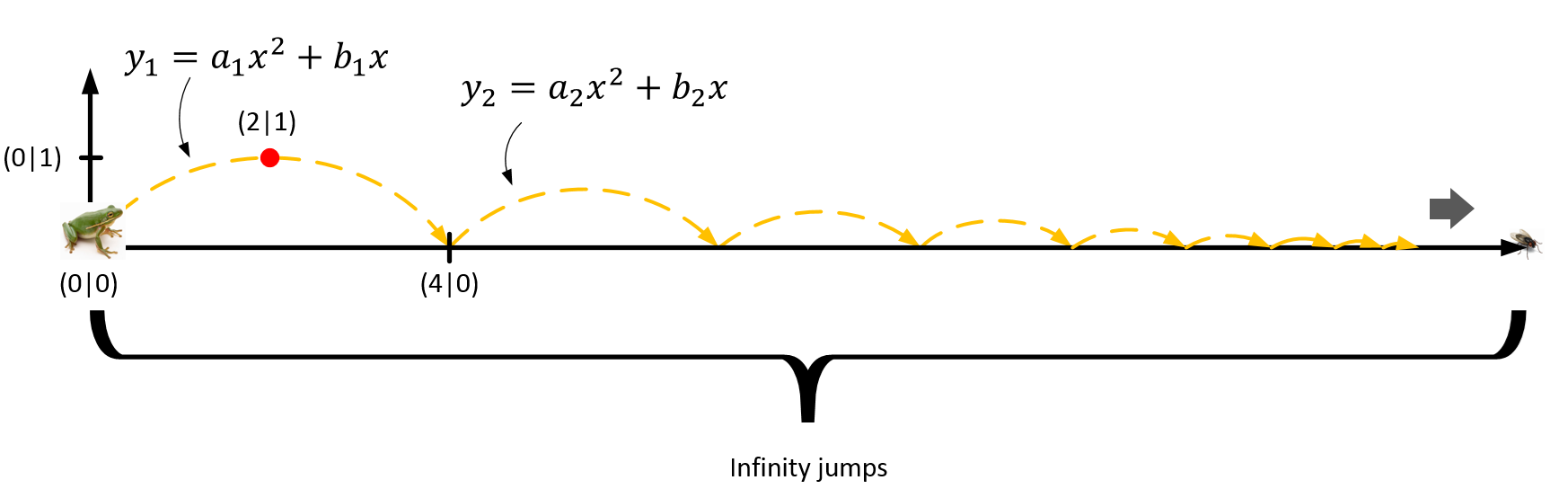
A frog sees a dead fly at the ground in some distance and jumps in consecutive jumps towards it. The trajectory of the frog can be modelled by parabolas . The horizontal length and the maximum height of each jump form a geometric progression , such that each jump will have 3/4 length and 2/3 height of the previous jump and the frog will reach the fly in ∞ jumps . After the first jump the frog travelled 4 cm horizontally and passed through a maximum at P (2|1) .
Calculate the length of the whole trajectory of all jumps till the frog reaches the fly.
Note: You may need to use a CAS for computations
The answer is 17.489.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let each parabola y n (starting from n = 0 ) be centred at the origin with the vertex at ( 0 , h n ) where h n is the maximum height of the jump, and cutting the x-axis at 2 l n and − 2 l n where l n is the horizontal length of the jump. This gives each parabola the following equation, which can be found by letting y = a x 2 + b and finding appropriate values for a and b such that the above conditions hold. y n = h n ( 1 − l n 2 4 x 2 ) l 0 = 4 , and l n = 4 3 l n − 1 , therefore l n = 4 ( 4 3 ) n
h 0 = 1 , and h n = 3 2 h n − 1 , therefore h n = ( 3 2 ) n ∴ y n = ( 3 2 ) n ( 1 − ( 4 ( 4 3 ) n ) 2 4 x 2 ) = ( 3 2 ) n − ( 3 2 ) n ( 9 1 6 ) n 1 6 4 x 2 = ( 3 2 ) n − ( 2 7 3 2 ) n 4 x 2
Now, the formula for arc length is ∫ a b ( f ′ ( x ) ) 2 + 1 d x . Call the length of the trajectory of one parabola T n . T n = ∫ − 2 l n 2 l n ( d x d y n ) 2 + 1 d x = 2 ∫ 0 2 l n ( − ( 2 7 3 2 ) n 2 x ) 2 + 1 d x = 2 ∫ 0 2 ( 4 3 ) n ( 2 7 3 2 ) 2 n 4 x 2 + 1 = ( 2 7 3 2 ) n ∫ 0 2 ( 4 3 ) n x 2 + 4 ( 3 2 2 7 ) 2 n = ( 2 7 3 2 ) n ⎣ ⎡ 2 x x 2 + 4 ( 3 2 2 7 ) 2 n + 2 ( 3 2 2 7 ) 2 n ln ∣ ∣ ∣ ∣ ∣ ∣ x + x 2 + 4 ( 3 2 2 7 ) 2 n ∣ ∣ ∣ ∣ ∣ ∣ ⎦ ⎤ 0 2 ( 4 3 ) n using ∫ x 2 + a 2 = 2 x x 2 + a 2 + 2 a 2 ln ∣ ∣ x + x 2 + a 2 ∣ ∣ = ( 4 3 ) n ( 2 7 3 2 ) n 4 ( 1 6 9 ) n + 4 ( 3 2 2 7 ) 2 n + 2 ( 3 2 2 7 ) n ln ⎝ ⎛ 2 ( 4 3 ) n + 4 ( 1 6 9 ) n + 4 ( 3 2 2 7 ) 2 n ⎠ ⎞ − 2 ( 3 2 2 7 ) n ln ( 2 ( 3 2 2 7 ) n ) = 2 ( 4 3 ) n 1 + ( 8 9 ) 2 n + 2 ( 3 2 2 7 ) n ln ⎝ ⎛ ( 9 8 ) n + 1 + ( 9 8 ) 2 n ⎠ ⎞
The total length of the trajectory of the frog will be n = 0 ∑ ∞ T n , but since this is rather complicated we may just evaluate this with a computer program, and get a result of 1 7 . 4 8 9