From an inequality to solving equations
x and y are integers such that:
⎩ ⎪ ⎨ ⎪ ⎧ A = x 4 + 8 x 3 + 2 6 x 2 + 4 0 x + 2 4 B = y 4 + 4 y 3 + 8 y 2 + 8 y + 3 C = x 4 + 8 x 3 + 3 0 x 2 + 5 6 x + 4 8
If A < B < C , how many different solutions are there?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let X = ( x + 2 ) 2 , Y = ( y + 1 ) 2 . So X and Y are nonnegative, and the inequalities in the problem become X 2 + 2 X < Y 2 + 2 Y < X 2 + 6 X + 8 . That is, X 2 + 2 X < Y 2 + 2 Y < ( X + 2 ) 2 + 2 ( X + 2 ) . Since f ( x ) = x 2 + 2 x is an increasing function on the nonnegative real numbers, this implies that X < Y < X + 2 . So Y = X + 1 .
This means ( y + 1 ) 2 − ( x + 2 ) 2 = 1 , and the only integral squares that differ by 1 are 0 and 1 , so ( y + 1 ) 2 = 1 and ( x + 2 ) 2 = 0 , which leads to the 2 solutions ( − 2 , 0 ) , ( − 2 , − 2 ) .
Let us first factorize A , B , and C .
A ( x ) = x 4 + 8 x 3 + 2 6 x 2 + 4 0 x + 2 4 = x 4 + 8 x 3 + 2 4 x 2 + 3 2 x + 1 6 + 2 x 2 + 8 x + 8 = ( x + 2 ) 4 + 2 ( x + 2 ) 2
We note that A ( x ) is symmetrical about x = − 2 , where it has its minimum value of 0 .
B ( y ) = y 4 + 4 y 3 + 8 y 2 + 8 y + 3 = y 4 + 4 y 3 + 6 y 2 + 4 y + 1 + 2 y 2 + 4 y + 2 = ( y + 1 ) 4 + 2 ( y + 1 ) 2
We note that B ( y ) has the same form as A ( x ) but symmetrical about y = − 1 , where it has its minimum value of 0 . In fact B ( x ) = A ( x − 1 ) and all the integer values of A ( x ) and B ( y ) are the same.
C ( x ) = x 4 + 8 x 3 + 3 0 x 2 + 5 6 x + 4 8 = x 4 + 8 x 3 + 2 6 x 2 + 4 0 x + 2 4 + 4 x 2 + 1 6 x + 2 4 = A ( x ) + 4 ( x + 2 ) 2 + 8
Again we find C ( x ) is symmetrical about x = − 2 , where it has its minimum value of \8). C ( x ) > A ( x ) for all x and the difference 4 ( x + 2 ) 2 + 8 increases with ∣ x + 2 ∣ .
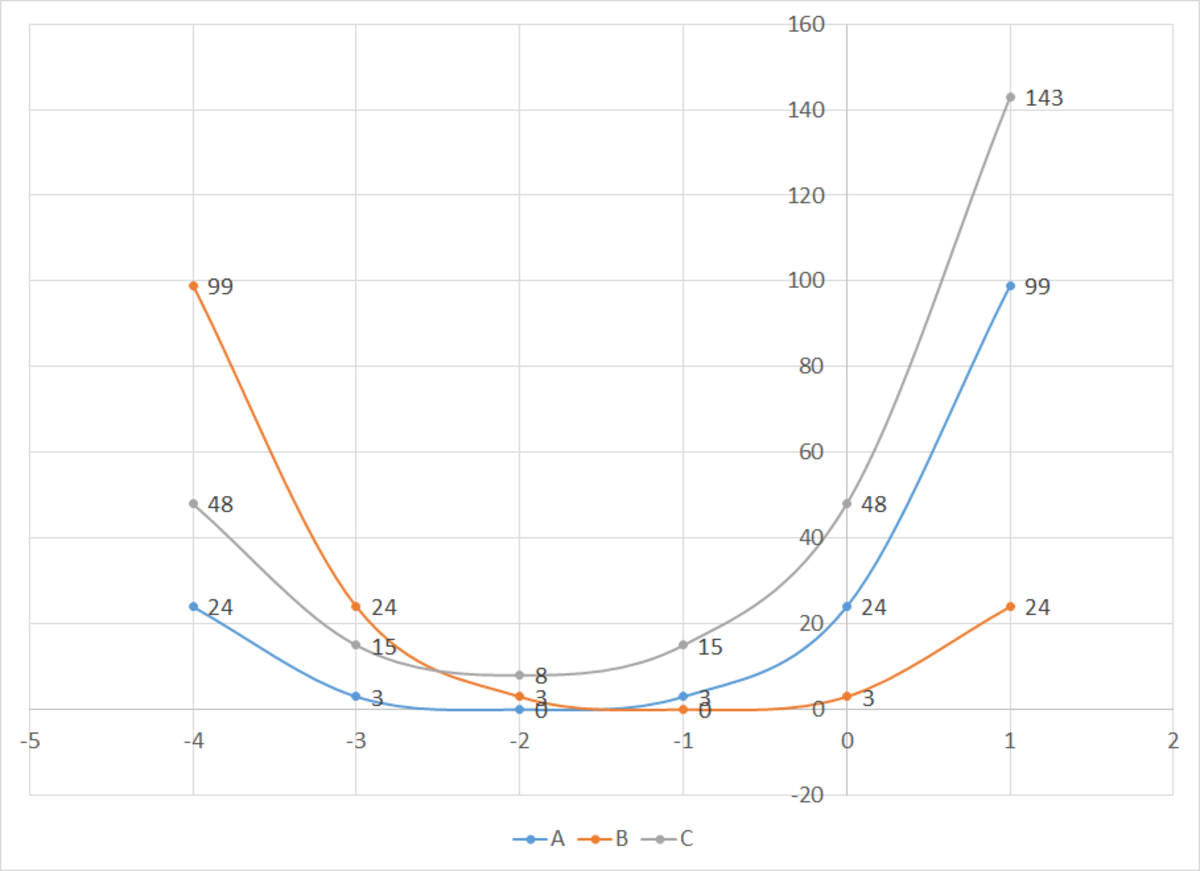
Plotting the graphs of A ( x ) , B ( x ) , and C ( x ) , we find that only A ( − 2 ) = 0 < B ( − 2 ) = B ( 0 ) = 3 < C ( 0 ) = 8 satisfy the condition. Therefore there are 2 solution pairs ( 0 , − 2 ) and ( 0 , 0 ) .
Sir, I don't think ( 0 , 0 ) is a solution.
Log in to reply
It is. We want A ( x ) = 0 , B ( y ) = 3 , and C ( x ) = 8 . It is clear that x = 0 because 0 and 8 are the minimum values of A and C respectively and they occur when x = 0 . For B ( y ) = ( y + 1 ) 4 + 2 ( y + 1 ) 2 = 3 , ⟹ ( y + 1 ) 2 = 1 ⟹ y = − 2 , 0 . Therefore the answer are ( x , y ) = ( 0 , − 2 ) , ( 0 , 0 ) .
Simplifying A , B , C , we have:
A = x 4 + 8 x 3 + 2 6 x 2 + 4 0 x + 2 4 = ( x 4 + 1 6 x 2 + 1 6 + 8 x 3 + 8 x 2 + 3 2 x ) + ( 2 x 2 + 8 x + 8 )
= ( x 2 + 4 x + 4 ) 2 + 2 ( x 2 + 4 x + 4 ) = ( x 2 + 4 x + 4 ) ( x 2 + 4 x + 6 )
B = y 4 + 4 y 3 + 8 y 2 + 8 y + 3 = ( y 4 + 4 y 2 + 1 + 4 y 3 + 2 y 2 + 4 y ) + ( 2 y 2 + 4 y + 2 )
= ( y 2 + 2 y + 1 ) 2 + 2 ( y 2 + 2 y + 1 ) = ( y 2 + 2 y + 1 ) ( y 2 + 2 y + 3 )
C = x 4 + 8 x 3 + 3 0 x 2 + 5 6 x + 4 8 = ( x 4 + 1 6 x 2 + 3 6 + 8 x 3 + 1 2 x 2 + 4 8 x ) + ( 2 x 2 + 8 x + 1 2 )
= ( x 2 + 4 x + 6 ) 2 + 2 ( x 2 + 4 x + 6 ) = ( x 2 + 4 x + 6 ) ( x 2 + 4 x + 8 )
Assuming there are integers a , b such that a = x 2 + 4 x + 4 , b = y 2 + 2 y + 1 , we have:
A < B < C ⇔ a ( a + 2 ) < b ( b + 2 ) < ( a + 2 ) ( a + 4 )
a ( a + 2 ) < b ( b + 2 ) ⇔ a 2 + 2 a < b 2 + 2 b ⇒ a 2 − b 2 + 2 a − 2 b < 0 ⇔ ( a − b ) ( a + b + 2 ) < 0
b ( b + 2 ) < ( a + 2 ) ( a + 4 ) ⇔ b 2 + 2 b < ( a + 2 ) 2 + 2 ( a + 2 ) ⇒ b 2 − ( a + 2 ) 2 + 2 b − 2 ( a + 2 ) < 0 ⇔ ( b − a − 2 ) ( a + b + 4 ) < 0
We have to solve the inequality { ( a − b ) ( a + b + 2 ) < 0 ( b − a − 2 ) ( a + b + 4 ) < 0
Examining each case will help us solve this inequality.
Case 1: a + b + 2 < − 2 ( < 0 ) ⇔ a + b + 4 < 0
⇒ { a − b > 0 b − a − 2 > 0 ⇔ a − b < − 2
This is clearly a contradiction since there is no such pair of ( a , b ) satisfying 0 < a − b < − 2 .
Case 2: a + b + 2 = − 2 ⇔ a + b + 4 = 0 (Contradiction, since 0 < 0 is false.)
Case 3: a + b + 2 = − 1 ⇔ { a + 3 = − b a + 1 = − ( b + 2 ) ⇒ ( a + 1 ) ( a + 3 ) = b ( b + 2 )
Case 4: a + b + 2 > 0 ⇔ a + b + 4 > 0 ⇒ { a − b < 0 ⇔ a < b b − a − 2 < 0 ⇔ b < a + 2 ⇔ a < b < a + 2
⇔ b = a + 1 ⇒ b ( b + 2 ) = ( a + 1 ) ( a + 3 )
Examining all cases, we can conclude that ( a + 1 ) ( a + 3 ) = b ( b + 2 ) .
Substitute a = x 2 + 4 x + 4 , b = y 2 + 2 y + 1 in ( a + 1 ) ( a + 3 ) = b ( b + 2 ) , we have:
( x 2 + 4 x + 5 ) ( x 2 + 4 x + 7 ) = ( y 2 + 2 y + 1 ) ( y 2 + 2 y + 3 )
⇔ ( x 2 + 4 x + 5 ) 2 + 2 ( x 2 + 4 x + 5 ) = ( y 2 + 2 y + 1 ) 2 + 2 ( y 2 + 2 y + 1 )
⇔ [ ( y 2 + 2 y + 1 ) 2 + 2 ( y 2 + 2 y + 1 ) + 1 ] − [ ( x 2 + 4 x + 5 ) 2 + 2 ( x 2 + 4 x + 5 ) + 1 ] = 0
⇔ ( y 2 + 2 y + 2 ) 2 − ( x 2 + 4 x + 6 ) 2 = 0
⇔ ( y 2 + 2 y + 2 − x 2 − 4 x − 6 ) ( y 2 + 2 y + 2 + x 2 + 4 x + 6 ) = 0
⇔ [ ( y + 1 ) 2 − ( x + 2 ) 2 − 1 ] [ ( y + 1 ) 2 + ( x + 2 ) 2 + 3 ] = 0
As ( y + 1 ) 2 + ( x + 2 ) 2 + 3 ≥ 3 > 0 , ( y + 1 ) 2 − ( x + 2 ) 2 − 1 = 0
⇔ ( y + x + 3 ) ( y − x − 1 ) = 1
Solving the equation gives us 2 solutions: ( x , y ) = ( − 2 , − 2 ) , ( − 2 , 0 )
Substitute these results in the original problem, we can see that these 2 pairs satisfy the conditions.
Hence there are 2 different solutions, which are ( x , y ) = ( − 2 , − 2 ) , ( − 2 , 0 )