From Toronto To Kabul
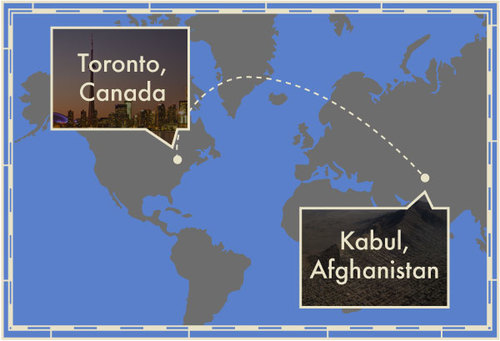 Make the simplifying assumption that the earth as a sphere with a radius of 6371 km. Find the length (in km) of the geodesic (shortest distance along the surface of the earth) between Toronto, Canada (43°39′N 79°23′W) and Kabul, Afghanistan (34°31′N 69°12′E).
Make the simplifying assumption that the earth as a sphere with a radius of 6371 km. Find the length (in km) of the geodesic (shortest distance along the surface of the earth) between Toronto, Canada (43°39′N 79°23′W) and Kabul, Afghanistan (34°31′N 69°12′E).
Details and assumptions
This problem accompanies the Around The World in 80 Hours competition.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Use Haversine formula , set distance, d as the subject
d = 2 r arcsin ( sin 2 ( 2 Δ ϕ ) + cos ( ϕ 1 ) cos ( ϕ 2 ) sin 2 ( 2 Δ λ ) )
r = 6 3 7 1 , Δ ϕ = 4 3 ∘ 3 9 ′ − 3 4 ∘ 3 1 ′ , Δ λ = 7 2 ∘ 2 3 ′ + 6 9 ∘ 1 2 ′
Convert measurements to radians and solve it, you should get 1 0 7 5 9 round up to the nearest integer.
What does the arc mean after 2r??
Log in to reply
if y = sin(x), then x = arcsin(y), where -pi < x < pi
The geodesic on a sphere is the great circle distance, which means a circle on the surface of the sphere whose center coincides with the center of the sphere.
Given this fact, the distance, d , will be equal to the central angle between the two points, θ , times the radius of the sphere, r . In this case, that gives us d = 6 3 7 1 × θ (assuming the angle is expressed in radians).
To find the central angle between two points on the surface of the sphere using latitude ( L ) and longitude ( λ ) , we use the spherical law of cosines:
θ = arccos ( sin L 1 sin L 2 + cos L 1 cos L 2 cos ( λ 1 − λ 2 ) )
Since the latitude and longitude are currently in D ∘ M'S'' (degrees, minutes, seconds) we'll want to convert them to radians (turning S and W into negative numbers to represent the different between them appropriately):
*Toronto: * L 1 = 4 3 ∘ 3 9 ′ N = 4 3 ∘ + 6 0 3 9 ∘ = 4 3 . 6 5 ∘ ≈ . 7 6 1 8 3 6 2 radians λ 1 = 7 9 ∘ 2 3 ′ W = − ( 7 9 ∘ + 6 0 2 3 = − 7 9 . 3 8 3 3 ∘ ≈ − 1 . 3 8 5 5 0 0 5 radians
*Kabul: * L 2 = 3 4 ∘ 3 1 ′ N = 3 4 ∘ + 6 0 3 1 ∘ = 3 4 . 5 1 6 6 ∘ ≈ . 6 0 2 4 2 9 4 8 radians λ 2 = 6 9 ∘ 1 2 ′ E = 6 9 ∘ + 6 0 1 2 = 6 9 . 2 ∘ ≈ 1 . 2 0 7 7 6 7 8 radians
Applying the above to the spherical law of cosines:
θ = arccos ( sin ( . 7 6 1 8 3 ) sin ( . 6 0 2 4 2 9 ) + cos ( . 7 6 1 8 3 ) cos ( . 6 0 2 4 2 9 ) ) cos ( 2 . 5 9 3 2 7 ) ) ≈ 1 . 6 8 8 7 3 4 radians
Thus the geodesic between these two cities is d ≈ 6 3 7 1 × 1 . 6 8 8 7 3 4 ≈ 1 0 7 5 9 km.
Note: For those who chose 10783 because Wolfram (or otherwise) told you so, the discrepancy is because Earth isn't perfectly spherical.