From volume to surface area
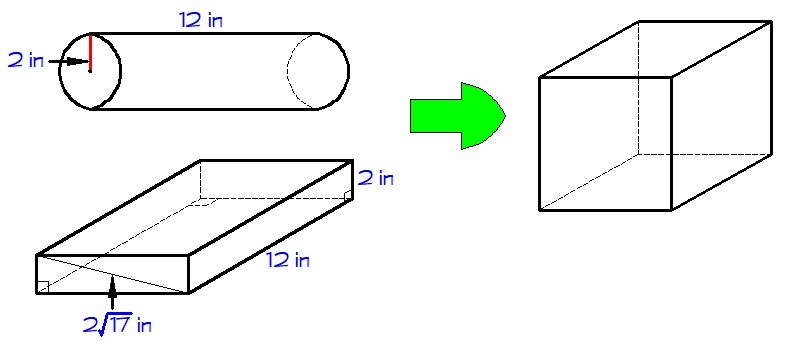 A right circular cylinder and a right prism with dimensions as shown are melted to form a cube. What is the surface area of the cube (in square feet)? Give your answer to the nearest integer. Take
A right circular cylinder and a right prism with dimensions as shown are melted to form a cube. What is the surface area of the cube (in square feet)? Give your answer to the nearest integer. Take
Note:
“in” means inches
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Here : Volume of Cube = Volume of cylinder + Volume of Cuboid Now in the cuboid , the third dimension comes out to be 8 inches by applying pythagoras in the diagonal . Hence it is 1 2 × 2 × 8 dimensioned(inches).
Now volume of cuboid = V 1 = 1 2 1 2 ⋅ 1 2 2 ⋅ 1 2 8 = 9 1 cube feet
Similarly volume of cylinder = V 2 = π r 2 h = 7 2 2 ⋅ ( 1 2 2 ) 2 ⋅ 1 = 1 2 6 1 1 cube feet Now adding both we get 1 2 6 1 1 + 9 1 ≈ 5 1
Therefore , Volume of cube → V 3 = a 3 = 5 1 ⟹ a = 3 5 1 Hence required surface area → ⟹ S = 6 a 2 = 5 3 2 6 ≈ 2 square feet