Fruit Mania

Probability Level 3

In how many different ways can I eat 3 bananas, 2 oranges, 4 plums and 10 grapes?

Details and Assumptions :

  • All fruits of the same type are identical.

  • I have to eat all the fruit.

  • I can only eat one piece of fruit at once.

Image Credit: Flickr France-♥


The answer is 116396280.

View wiki
Melissa Quail by Melissa Quail , 21, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Samuel Ayinde
Apr 1, 2015

total fruit= 19 19

number of ways to eat those fruit = 19 ! 3 ! × 2 ! × 4 ! × 10 ! \frac{19!}{3!\times2!\times4!\times10!}

= 116396280 116396280

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Aquib Immanuel
Mar 31, 2015

If A out of N items are identical, then the number of different permutations of the N items is N!/A! If a set of N items contains A identical items, B identical items, and C identical items etc.., then the total number of different permutations of N objects is N!/(A!⋅B!⋅C!...!) here the answer would be

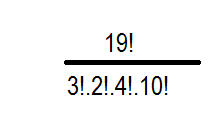
2 Helpful 0 Interesting 0 Brilliant 0 Confused

For those who aren't familiar with the formula, let me explain in brief why the formula works!

When we are considering n ! n! ways, note that we're also permuting the identical items within the n ! n! arrangements. But permuting identical items result in getting the same arrangement which shouldn't be counted again. If there are x x types of items with r x r_x identical items of type x x , then while permuting, we originally counted each arrangement as ∏ x ( r i ) ! \displaystyle\prod_x (r_i)! arrangements because we permuted the identical r i r_i items in ( r i ) ! (r_i)! ways corresponding to each required arrangement and the product notation follows by the rule of product when we are taking all types into account.

Hence, since we counted n ! n! arrangements, the actual number of arrangements is n ! ∏ x ( r i ) ! \dfrac{n!}{\displaystyle\prod_x (r_i)!} by unitary method.

Prasun Biswas - 6 years, 2 months ago

Log in to reply

Nice note Prasun !

Venkata Karthik Bandaru - 6 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...