Number Theory with Finite State Machines
Assume that the strings accept by the automata below are interpreted as binary numbers .
What is the largest integer such that the set of integers accepted by the automata are always be divisible by ?
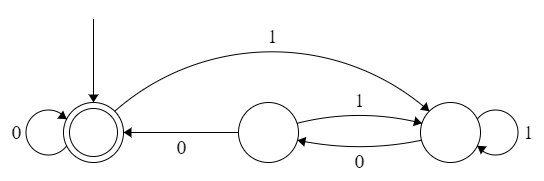
Clarification : Empty string is considered as equivalent to 0 in this question.
Extra Credit : Both this FSM and the one in Agnishom Chattopadhyay's question (linked below) has three states. But the answers are different. Account for this phenomenon.
Inspiration : Lexical Number Theory
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Expressing the FSM as a regular expression, using the ed format, it is ^(11 0(10) 0)$. That shows that it is either the null string which is defined as being zero which is divisible by any natural number or it ends in 00 which is divisible by 4. The remainder of the sequences when divided by 4 could be any odd natural number, which includes primes.