Fun with 2018 #6

Geometry Level 1

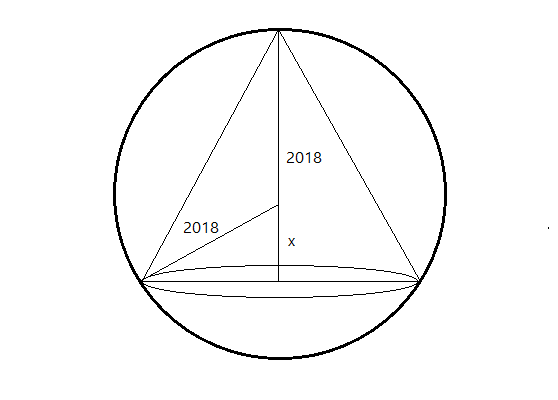
The biggest volume V V of a cone inscribed in a sphere of radius 2018 2018 can be written as V = 1 3 π ( 201 8 2 − x 2 ) ( 2018 + x ) V = \frac{1}{3} \pi (2018^2 - x^2)(2018 + x) where x = A B ⋅ 2018 x = \frac{A}{B} \cdot2018 with A , B A, B coprime positive integers. Enter 10 A + B + 5 10A + B + 5 .


The answer is 18.

Guillermo Templado by Guillermo Templado , 46, Spain

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Saya Suka
Jan 20, 2021

It's like how a largest tetrahedron is placed in a sphere, the central point distance from the peak is triple of that from the bottom face.
Answer
= 10(1) + (3) + 5
= 18


0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...