Foolish Fun with COM of an IIT JEE alien.

Classical Mechanics Level 5

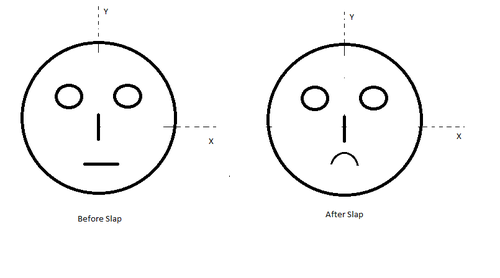A hypothetical alien lives on a hypothetical Planet and has a 2-dimensional face.

If he is made out of pieces of a homogeneous wire of uniform line thickness, and let mass of his two eyes (inner circles) is m m , and mass of the his nose and his lips is also m m each ( Vertical and horizontal lines ) also mass of boundary of his face is 6 m 6m .

The coordinates of the centres of the different parts are :

  • Outer circle ( Face Boundary ) is (0,0)
  • Left circle ( left eye ) is (-a,a)
  • Left circle ( Right eye ) is (a,a)
  • Vertical Line ( Nose ) is (0,0)
  • Horizontal Line ( Lips ) is (0,-a)

In this situation the y y -coordinate of the centre of mass of the alien is y o { y }_{ o } .

Then an friend of this alien give an slap to him due to their Personal matters. So This alien becomes sad and curls his lips about it's centre into a semi-circle of radius r r .

Then find the radius r r such that the new y y -coordinate of the centre of mass of this alien becomes − y o -{ y }_{ o } .

Details and Assumptions

  • a = 10 a=10
  • All body parts have uniform same mass density.

Note

This question is inspired from an question of IIT JEE 2009: Q-41
This is Part of set : Foolish things


The answer is 31.4.

Deepanshu Gupta by Deepanshu Gupta , 25, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Cody Martin
Feb 16, 2015

i n i t i a l l y initially y c m = m ( a ) + m ( a ) + 6 m ( 0 ) + m ( − a ) 10 m = a 10 y_{cm}=\frac{ m(a)+m(a)+6m(0)+m(-a) }{ 10m }=\frac{ a }{ 10 } f i n a l l y finally − a 10 = m ( a ) + m ( a ) + 6 m ( 0 ) + m ( a − 2 r π ) 10 m \frac{ -a }{ 10 }=\frac{ m(a)+m(a)+6m(0)+m(a-\frac{ 2r }{ \pi }) }{ 10m } a = − r π a=\frac{ -r }{ \pi } r = 10 ∗ 3.14 = 31.4 r=10*3.14= 31.4

6 Helpful 0 Interesting 0 Brilliant 0 Confused

Ohh , I did wrongly assume that a = 1 a=1 , hence I got answer as π \pi . So i repetedly entering pi or pi/2 or 2pi , but fails ....

But anyway , This is really funny ! I really like you problem making skills

Nishu sharma - 6 years, 1 month ago

There is a slight mistake in the solution @Cody Martin , In the second expression, the last term should be m ( − a − 2 r / π ) m(-a-2r/\pi) then solving we will get r = a π r={a}{\pi}

R G Staff - 4 years, 6 months ago

The alien should be a masochist and should be happy rather than sad To make the y-coordinate of the com of the circle(lip) go lower than its initial position :P

Suhas Sheikh - 2 years, 10 months ago

Bozzo!!!! :P

Rudra Gupta - 6 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...