Fun with conics
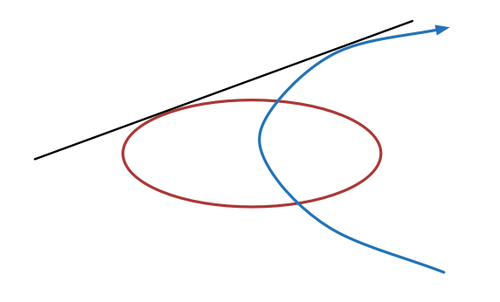 Consider the parabola
y
2
=
4
x
and the ellipse
9
x
2
+
4
y
2
=
1
.
Consider the parabola
y
2
=
4
x
and the ellipse
9
x
2
+
4
y
2
=
1
.
The tangent line of positive slope that is common to these two curves has a y -intercept of the form a + b , where a and b are positive integers and b is square-free. Find a + b .
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
wow what a solution ! And Sir Can you tell me please that , what is pedal curve ? Thanks !
Log in to reply
This may not be very formal or even precise, but here is what I understand: It is the locus of the foot of the perpendicular drawn from a point to the tangents to a curve. i remember it as "Pedal is where the foot rests" :-) E.g. for a parabola, if we drop perpendiculars from the focus to various tangents, then all the points of such perpendicularity form a straight line which is the tangent at the vertex. I am sure there is more to it and I encourage you to look up the formal definition.
This is an elegant solution, Ujjwal. Thank you for posting it. I hadn't heard of the pedal curve before; good to know. :)
Log in to reply
Thanks Brian! I must admit, I did not know about it either. Came across this quiet accidentally as I was trying to find constructions for triangles when different combinations of data are given. Then discovered that in general such loci are called Pedal curves! See around 6:35 minute mark in this video on triangle contruction
I love the way you did that. I saw such a solution for the first time.
Really awesome, Ujjwal.
This one was quite easier.
General equation of tangent of slope m for
-
parabola y 2 = 4 a x is y = m x + m a
-
ellipse a 2 x 2 + b 2 y 2 = 1 is y = m x ± a 2 m 2 + b 2
So tangents in these cases would be y = m x + m 1 and y = m x ± 9 m 2 + 4 .
Comparing both the equations,
m 2 ( 9 m 2 + 4 ) = 1
On solving we get m 1 = 2 + 1 3
Nice approach, Pranjal, but I think that you mean that m 1 = 2 + 1 3 .
Nice solution, but is there a general equation for the tangent to a parabola case for b , c = 0 . And also for the ellipse where r 2 = 1
Log in to reply
For the parabola, you need to complete the square and then shift the origin.
For example, take the parabola y 2 − 8 y + 1 2 = 4 x . You need to write it as y 2 − 8 y + 1 6 = 4 x + 4 , that is, ( y − 4 ) 2 = 4 ( x + 4 ) and then substitute X = x + 4 , Y = y − 4 .
I am not sure what you mean by "an ellipse with r 2 = 1 ".
I did this by writing equation of tangents of given parabola and ellipse in parametric form and comparing to eliminate assumed parameters.
Let's 'stretch' or scale up the the problem in the Y direction by a factor of 3/2, thus simplifying the given ellipse and parabola into a circle x 2 + y 2 = 9 and a parabola y 2 = 9 x = 4 ( 4 9 ) x with focus F = ( 4 9 , 0 )
Let T 1 ( h , k ) , T 2 be points of tangency. Then foot of perpendicular P from F on the tangent must lie on the Y axis (= tangent at the vertext = the pedal* curve here!)
Another property of Parabola gives X-intercept of tangent = -h and therefore Y-intercept as k/2
From the two similar triangles formed: O T 2 P and P O F :
P F O P = O P O T 2 ( 9 / 4 ) 2 + ( k / 2 ) 2 k / 2 = k / 2 3 Giving the equation k 4 − 3 6 k − 7 2 9 = 0 solving which we get the Y-Intercept k/2 as 2 3 2 + 1 3
But this is for the 'stretched' problem of circle and another parabola, so let us shrink it back by a factor of 2/3 to get the desired Y-intercept as 2 + 1 3