Fun with infinite sets

Geometry Level 1

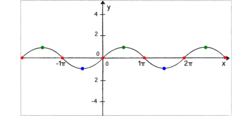Imagine the graph of function the $f(x)=\sin(x).$ The domain of this function is the set of all real numbers $R.$

Consider the three sets

$A=\left\{ x\in \mathbb R|\sin(x)=-1 \right\}$
$B=\left\{ x\in \mathbb R|\sin(x)=0 \right\}$
$C=\left\{ x\in \mathbb R|\sin(x)=1 \right\}.$

Which of them has the largest cardinality?

A B C All of them have the same cardinality

4 solutions

Kay Xspre
Sep 11, 2015

I can prove only in the case $x$ be integer that the member of A will satisfy $\frac{\pi}{2}(3+4x)$ , B will satisfy $x\pi$ and C will satisfy $\frac{\pi}{2}(1+4x)$ . Given that the integer is an infinite set, A, B and C will also be infinite set.

Can the option be B because from the graph we can see that 0 is included and adds one more to the cardinality , I mean:

B = { 0 , $\pi$ , 2 $\pi$ } ,

However, all other sets are : A,C = { $\pm \frac{\pi}{2}$ , $\pm \frac{3 \pi}{2}$ , ...... }

Syed Baqir - 5 years, 9 months ago

Not with the definition of cardinality.

Two sets $A$ and $B$ are said to have the same cardinality if there exists a bijection $A \to B$ .

One possibility is $y=2x-\pi$ with $x\!\in\!A\space\& \space y\!\in\!B$

Jerry McKenzie - 4 years ago

The Rational Thinker .
Jan 9, 2019

Sine is a periodic function, meaning that it repeats itself at interger multiples of 2*pi. So a way to think of it is just purely about it's interger parts. Another thing you will notice is that it seems as though there are twice as many that crosses zero as oppose to one. Well we could actually say that there are just as many points that pass through zero as there are points that equal 1. And same goes for -1.

How? Imagine if I asked you to tell me why there are an equal amount of sheeps and cows. The reason why we say they are equal is because for every cow, we can also pair it up with a sheep with a 1 to 1 correspondence. If I told you to tell me if I can pair all the natural numbers with all the even number, all one has to do is pair every natural number n to 2n. You can also pair every interger with every natural number. Let's try that. {1,-1,2,-2,3,-3,....} We can pair 1 with 1, 2 with -1, 3 with -2, and so on.

Now let's apply our pairing game to this. It becomes clear how we can pair all the points where f(x)=0 and all the points where f(x)=1. Same goes for -1.

Stephen Donovan
May 24, 2021

I’m on mobile so I won’t type too much, but for anyone who’s struggling with this question, it will likely help if you instead show that there’s a bijection between each set and the integers, and then you can pretty easily make a bijection between any two of the sets.

Swayam Prakash Kar
Sep 23, 2020

Given f(x)= sinx is a trignometric function which is a periodic function with a principal range of [-1,1]. It repeats in every interval of 2pi and have a general solution 2npi +_ x. Therefore, each of them repeats at each interval with the given values 3pi/2 +_ 2npi=(-1) , 2npi=0 and pi/2+_ 2npi = 1.

Fun with infinite sets

4 solutions

0 pending reports