Fun with series 1

Algebra Level 2

The value of

1 11 × 13 + 1 13 × 15 + 1 15 × 17 + 1 17 × 19 + 1 19 × 21 + 1 21 × 23 + 1 46 \frac{1}{11\times13}+\frac{1}{13\times15}+\frac{1}{15\times17}+\frac{1}{17\times19}+\frac{1}{19\times21}+\frac{1}{21\times23}+\frac{1}{46}

is m n \frac{m}{n} for relatively prime m m and n n . Find m + n m+n .


The answer is 23.

Tom Zhou by Tom Zhou , 21, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Parveen Soni
Nov 1, 2014

multiply and divide whole series by 2 and we get and rewrite each term as
subtraction of two numbers 2/(11x13)=1/11-1/13 and drop the same terms with opposite sign.finally we have (1/2)x(11) as answer i.e m=1 and n=22
answer=22+1=23

1 Helpful 0 Interesting 0 Brilliant 0 Confused

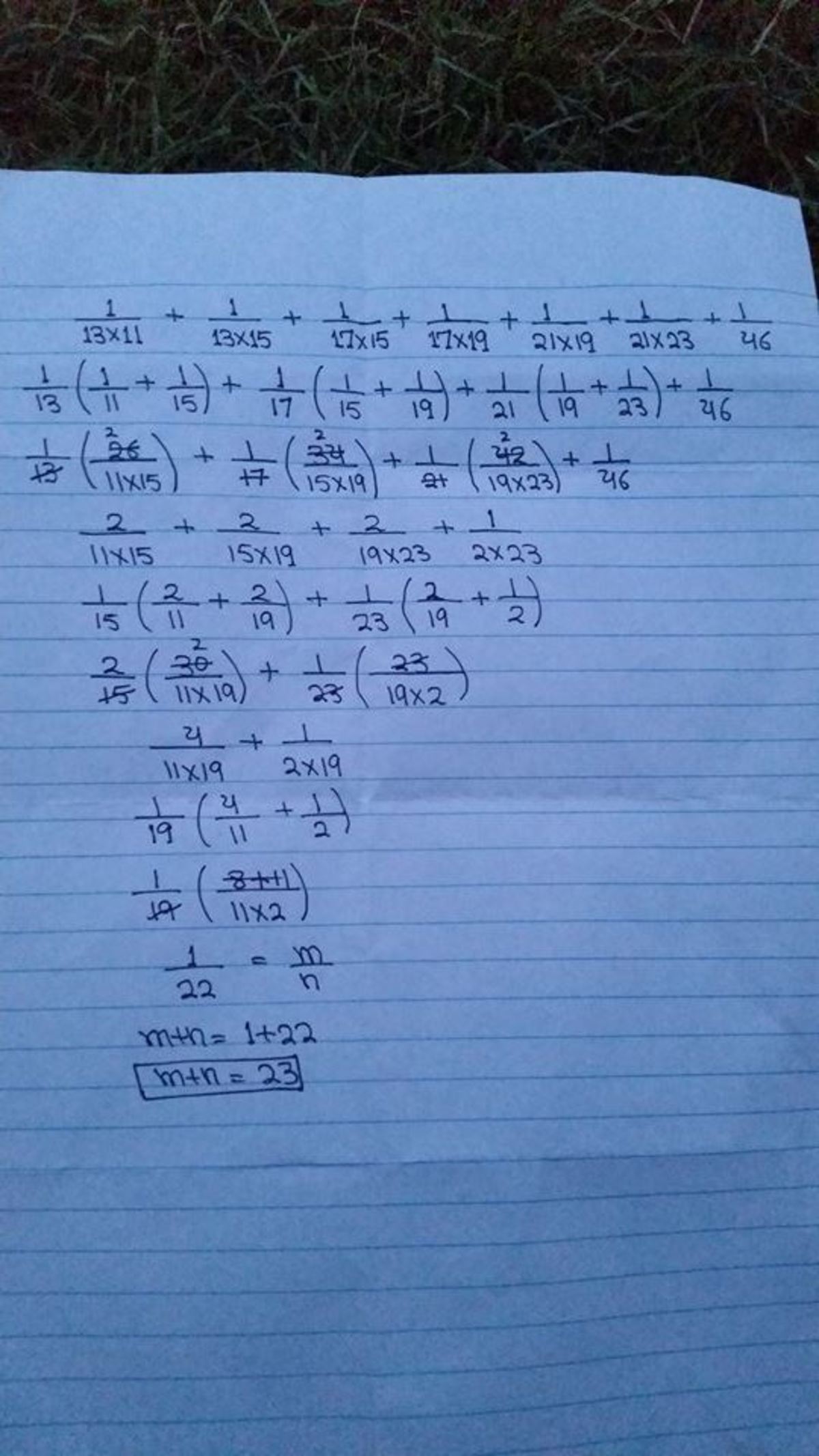take same terms as common from the denominator of each two consecutive terms and find the value of the inner terms in this way continue solving you will get 1/22 and by adding 1 and 22 we get 23.i will soon upload the solution set as image.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...