Fun with sin^6 summation

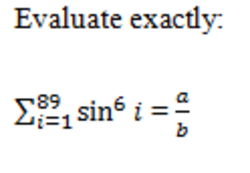
$S = \sin ^{ 6 }{ 1 } + \sin ^{ 6 }{ 2 } + ... + \sin ^{ 6 }{ 88 } + \sin ^{ 6 }{ 89 }$

Keeping in mind that $sinX = cos(90-X)$ , this means $sin^{ 6 } X = cos^{ 6 } (90-X)$

Therefore we have our sum:

$S = \sin ^{ 6 }{ 1 } + \sin ^{ 6 }{ 2 } + ... + \sin ^{ 6 }{ 44} + \sin ^{ 6 }{ 45 } + \cos^{ 6 }(90 - 46) + ... + \cos^{ 6 }(90 - 88) + \cos^{ 6 }(90 - 89)$

Which simplifies to:

$S = \sin ^{ 6 }{ 1 } + \sin ^{ 6 }{ 2 } + ... + \sin ^{ 6 }{ 44} + \sin ^{ 6 }{ 45 } + \cos^{ 6 }{ 44 } + ... + \cos^{ 6 }{ 2 } + \cos^{ 6 }{ 1 }$

Since,

$\sin45 = \frac{\sqrt{2}}{2}$ then, $\sin ^{ 6 }{ 45 } = \frac{1}{8}$ and also,

$\sin ^{ 6 }{ X } + \cos ^{ 6 }{ X } = (1 - 3sin ^{ 2 }{ X }cos ^{ 2 }{ X })$

So going back to our sum:

$S = \sin ^{ 6 }{ 1 } + \sin ^{ 6 }{ 2 } + ... + \sin ^{ 6 }{ 88 } + \sin ^{ 6 }{ 89 }$

$S = (1 - 3sin ^{ 2 }{ 1 }cos ^{ 2 }{ 1 }) + (1 - 3sin ^{ 2 }{ 2 }cos ^{ 2 }{ 2 }) + ... + (1 - 3sin ^{ 2 }{ 44}cos ^{ 2 }{ 44 }) + \sin ^{ 6 }{ 45 }$

Adding all the ones and factoring out a -3: $S = 44 + \frac{1}{8} -3 (sin ^{ 2 }{ 1 }cos ^{ 2 }{ 1 } +sin ^{ 2 }{ 2 }cos ^{ 2 }{ 2 } + ... + sin ^{ 2 }{ 44}cos ^{ 2 }{ 44 })$

Since $sin 2X = 2sinXcosX$ , lets write the above equation as:

$S = 44 + \frac{1}{8} -\frac{3}{4} (4sin ^{ 2 }{ 1 }cos ^{ 2 }{ 1 } +4sin ^{ 2 }{ 2 }cos ^{ 2 }{ 2 } + ... + 4sin ^{ 2 }{ 44}cos ^{ 2 }{ 44 })$

We did this because $4sin^ {2}{ X }cos ^ {2} { X } = 2sin^{2} { 2X }$

Therefore our sum can be written, and simplified as:

$S = \frac{353}{8} -\frac{3}{4} (sin ^{ 2 }{ 2 } +sin ^{ 2 }{ 4 } + ... + sin ^{ 2 }{ 44} + sin ^{ 2 }{ 46} + ... + sin ^{ 2 }{ 88})$

$S = \frac{353}{8} -\frac{3}{4} (sin ^{ 2 }{ 2 } +sin ^{ 2 }{ 4 } + ... + sin ^{ 2 }{ 44} + cos ^{ 2 }{(90 - 46)} + ... + cos ^ {2} {(90 -86)} + cos ^{ 2 }{(90 - 88)})$

$S = \frac{353}{8} -\frac{3}{4} (sin ^{ 2 }{ 2 } +sin ^{ 2 }{ 4 } + ... + sin ^{ 2 }{ 44} + cos ^{ 2 }{44} + ... + cos ^ {2} {4} + cos ^{ 2 }{2})$

$S = \frac{353}{8} -\frac{3}{4} (sin ^{ 2 }{ 2 } + cos ^{ 2 }{2} +sin ^{ 2 }{ 4 } + cos ^ {2} {4} + ... + sin ^{ 2 }{ 44} + cos ^{ 2 }{44})$

And $sin ^{ 2 }{ X} + cos ^{ 2 }{X} = 1$ , therefore

$S = \frac{353}{8} -\frac{3}{4} (22)$

$S = \frac{353}{8} -\frac{132}{8}$

$S = \frac{221}{8}$

$S = 27.625$