Functional Equation
If f is a function satisfying f ( x + y ) = 3 y f ( x ) + 2 x f ( y ) for all x , y ∈ R and f ( 1 ) = 1 , what is the value of f ( 3 ) ?
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
very nice method. i like it but i solve it different method .
All we simply do is compute f ( 2 ) and use that for f ( 3 )
f ( 2 ) = f ( 1 + 1 ) = 3 f ( 1 ) + 2 f ( 1 ) = 5 f ( 1 ) = 5
f ( 3 ) = f ( 2 + 1 ) = 3 f ( 2 ) + 4 f ( 1 ) = 1 9
and we are done.
As a side note by inspection f ( x ) = 3 x − 2 x
I did it the same way. I'm wondering why is this level 3 when it may very well be 2.
please tell me complete solution with details i can't satisfy completely.
Great fun! Bears a strong analogy to the factorial function, as this code displays. Incidentally, f(10)=58025, just in case anyone wants to know.
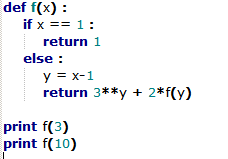
Love to see someone using python :-) Kudos points :-)
Log in to reply
Thank you. Like a tank to crack a walnut in this case.
first we compute f(2) and go for f(3)
given f(1)=1
f(2)=f(1+1)=3+2=5
f(3)=f(2+1)=19
First we substitute ( x ; y ) → ( x ; 1 ) . This gives us: f ( x + 1 ) = 3 f ( x ) + 2 x ⇔ f ( x ) = 3 f ( x − 1 ) + 2 x − 1 Next we define a new function g ( x ) such that: g ( x ) = f ( x ) + 2 x = 3 f ( x − 1 ) + 2 x − 1 + 2 . 2 x − 1 = 3 ( f ( x − 1 ) + 2 x − 1 ) = 3 g ( x − 1 ) This implies that for integer x g ( x ) is a geometric progression and g ( x ) = g ( 1 ) . 3 x − 1 . This can be extended to all real numbers. We are given f ( 1 ) = 1 and by the definition of g ( x ) we have g ( 1 ) = f ( 1 ) + 2 = 3 and so g ( x ) = 3 x . From the definition of g ( x ) we find: f ( x ) = g ( x ) − 2 x = 3 x − 2 x Therefore f ( 3 ) = 1 9 and this is our answer.
I know that @Ishan Tarunesh has a better and a more straightforward solution, but this is how I did it :)
f ( x + y ) = 3 y f ( x ) + 2 x f ( y )
Replace x and y with each other
f ( y + x ) = 3 x f ( y ) + 2 y f ( x )
Since LHS is same in both case, RHS must also be equal
2 x f ( y ) + 3 y f ( x ) = 3 x f ( y ) + 2 y f ( x )
Rearranging we get 3 x f ( y ) − 2 x f ( y ) = 3 y f ( x ) − 2 y f ( x )
Put y = 1 we get
f ( x ) = 3 x − 2 x
Now f(3) = 19