Functions 02
Given that the range of the function f ( x ) = x 2 + x 2 + 1 1 is in the interval [ a , ∞ ) , find the value of a .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
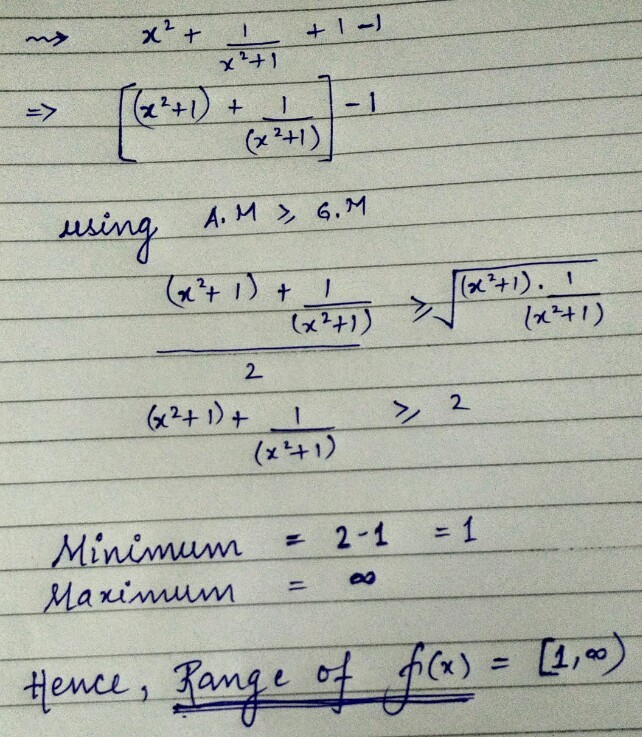
Done exactly the same
Good one .
There are multiple ways to do this, and as I try finding the extreme point, this solution also came up to me. For real number x , x 2 ≥ 0 , thus: x 2 + 1 ≥ 1 ; 0 < x 2 + 1 1 ≤ 1 When put x 2 in, it will be x 2 < x 2 + x 2 + 1 1 ≤ x 2 + 1 as 1 ≤ x 2 + 1 , the lowest possible value of f ( x ) is 1 from x = 0