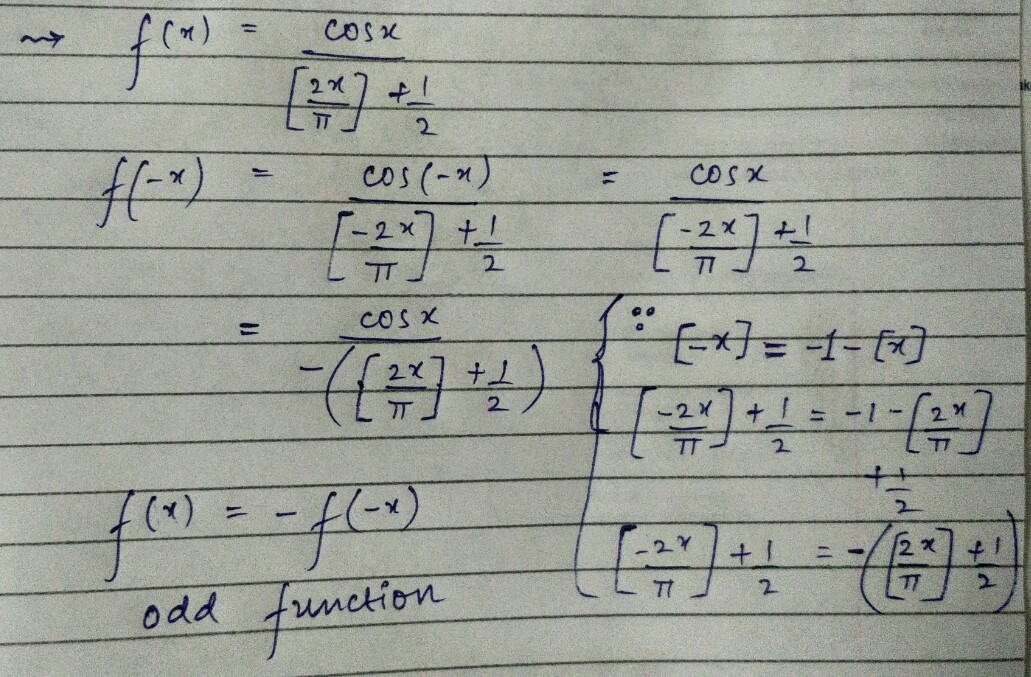Functions 05
f ( x ) = ⌊ π 2 x ⌋ + 2 1 cos x
What is the value of f ( x ) above for all x = n π , where n ∈ Z ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
f ( x ) = ⌊ π 2 x ⌋ + 2 1 cos x ⟹ f ( − x ) = ⌊ − π 2 x ⌋ + 2 1 cos ( − x ) = − 1 − ⌊ π 2 x ⌋ + 2 1 cos x = − ⌊ π 2 x ⌋ − 2 1 cos x = − ⌊ π 2 x ⌋ + 2 1 cos x = − f ( x ) cos ( − x ) = cos x ⌊ − y ⌋ = − 1 − ⌊ y ⌋ for y ∈ R ∖ Z
Thus f ( x ) is an odd function for any x which is not an integral multiple of π .
Hey Tapas, what if it is an odd integer, I mean it is already specified that it can't be an integer but look at this once, x = n π π 2 x = 2 n We had only proved here that it can't be even integer. What if it is odd, then it will be simultaneously odd and even.