Funky Star
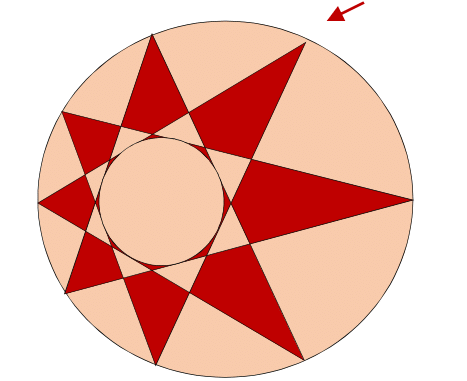 Find the measure of the star's internal angle at the point indicated.
Find the measure of the star's internal angle at the point indicated.
The radius of the small circle is 1. The large circle has a center on the small circle and its radius is 3. The vertices of the shortest and the longest arms of the star are on the line connecting the centers of the circles. The lines going to those points and to the point indicated by the arrow are tangent to the small circle. The star may not, in the end, connect quite as prettily as shown, but the above facts are sufficient to find the angle.
The answer is 32.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Yes! Nice. I think the diagram in the question has been framed intentionally to be misleading. \color\green{Mine} \color\green{a} \color\green{bit} \color\green{simpler} : Find BD, by drawing O P ⊥ A B . => B D = 1 2 . Then \angle CBD=arctan(\frac{1}{\sqrt{12}})\ = \(16.1^\circ Therefore our required angle should be 2 ∗ 1 6 . 1 ∘ = 3 2 . 2 ∘
Your solution assumes that one of the lines in the diagram is B O , where O is the center of the large circle. Why should this line pass through the center of the circle?
Log in to reply
The line BO is not one of the lines making up the star. It is a construction line made to go from the center to one of the points of the star. It is the angle DBC that is 1 6 . 1 ∘ , the angle CBO is slightly smaller. The angle at the point of the star is double the angle DBC, however, since the other line is also tangent to the same small circle.
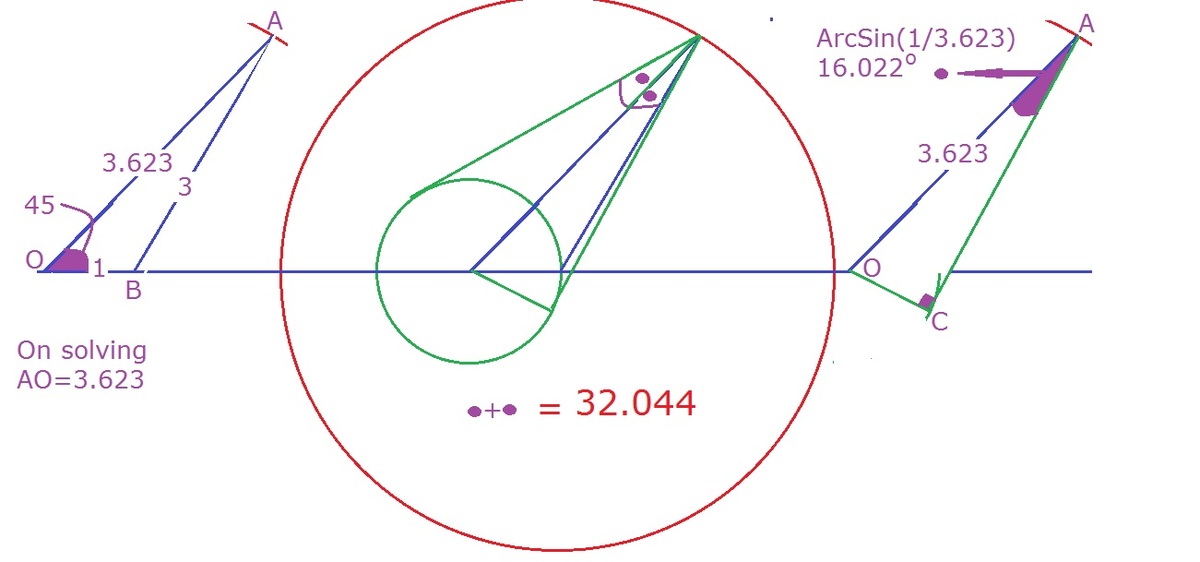
Triangle A O B is isosceles with ∠ O B A = ∠ O A B = 3 0 ∘ so ∠ A O B = 1 2 0 ∘ .
The distance C B can be obtained from the law of cosines applied to triangle C O B .
C B = 1 + 3 2 − 2 × 3 × c o s ( 1 2 0 ∘ ) = 1 3 .
From the right triangle C B D we get ∠ C B D = a r c s i n ( 1 3 1 ) ≈ 1 6 . 1 ∘ .
The internal angle we are seeking is double that, or 3 2 . 2 ∘ .