Funny Febo !
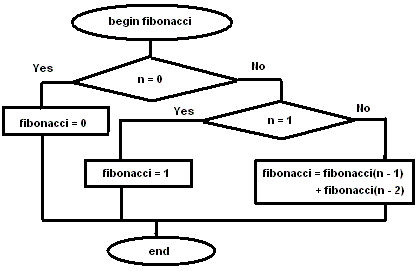
Assume a recursive function to find the Fibonacci term. What is the number of calls for that function to find the term?
Details and Assumptions:
- , and
- where
This problem is a part of the set: Efficient Algorithms .
The answer is 41.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 , 1 , 2 , 3 , 5 , 8 , 1 3 , 2 1 … The sequence given above is the Fibonacci sequence which can be generalize as:
F 0 = 1 , F 1 = 1 and F n = F n − 1 + F n − 2 where n ≥ 2 .
For exapmle: When we want to find F 2 we call the recursive function F 2 which then calls F 0 and F 1 . Hence we say the function is called thrice.
Here is a list which gives the Fibonacci sequence in the first column and the number of function calls to get it:
0 → 1
1 → 1
2 → 3
3 → 5
4 → 9
5 → 15
6 → 25
7 → 4 1
.
.
.
Since we know that to find n t h term we have to find ( n − 1 ) t h and ( n − 2 ) t h terms. Hence the first call of function is F(n) then the remaining calls for F(n-1) and F(n-2). Therefore N(F(n))=1+N(F(n-1))+N(F(n-2)).
The image below is a tree that shows the total number of function calls to find 6 t h term:
I hope that might help you understand the logic behind that function more clearly.