This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 ∠
C
E
B
=
1
8
0
−
7
0
−
2
0
−
6
0
=
3
0
∠
C
E
B
=
1
8
0
−
7
0
−
2
0
−
6
0
=
3
0
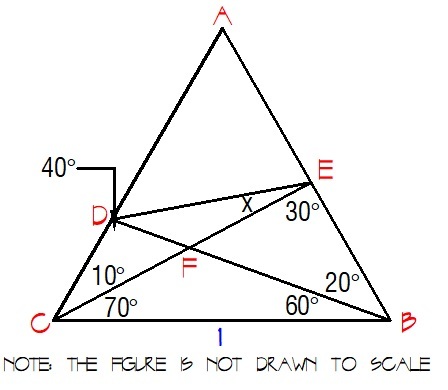
∠ B D C = 1 8 0 − 6 0 − 1 0 − 7 0 = 4 0
Let C B = 1 . Sine law on △ B C D .
sin 6 0 C D = sin 4 0 1 ⟹ C D ≈ 1 . 3 4 7
Sine law on △ B C E .
sin 8 0 C E = sin 3 0 1 ⟹ C E ≈ 1 . 9 7
Cosine law on △ C D E .
D E 2 = 1 . 9 7 2 + 1 . 3 4 7 2 − 2 ( 1 . 9 7 ) ( 1 . 3 4 7 ) ( cos 1 0 ) ⟹ D E ≈ 0 . 6 8 5
Sine law on △ C D E .
1 . 3 4 7 sin x = 0 . 6 8 5 sin 1 0 ⟹ x = 2 0
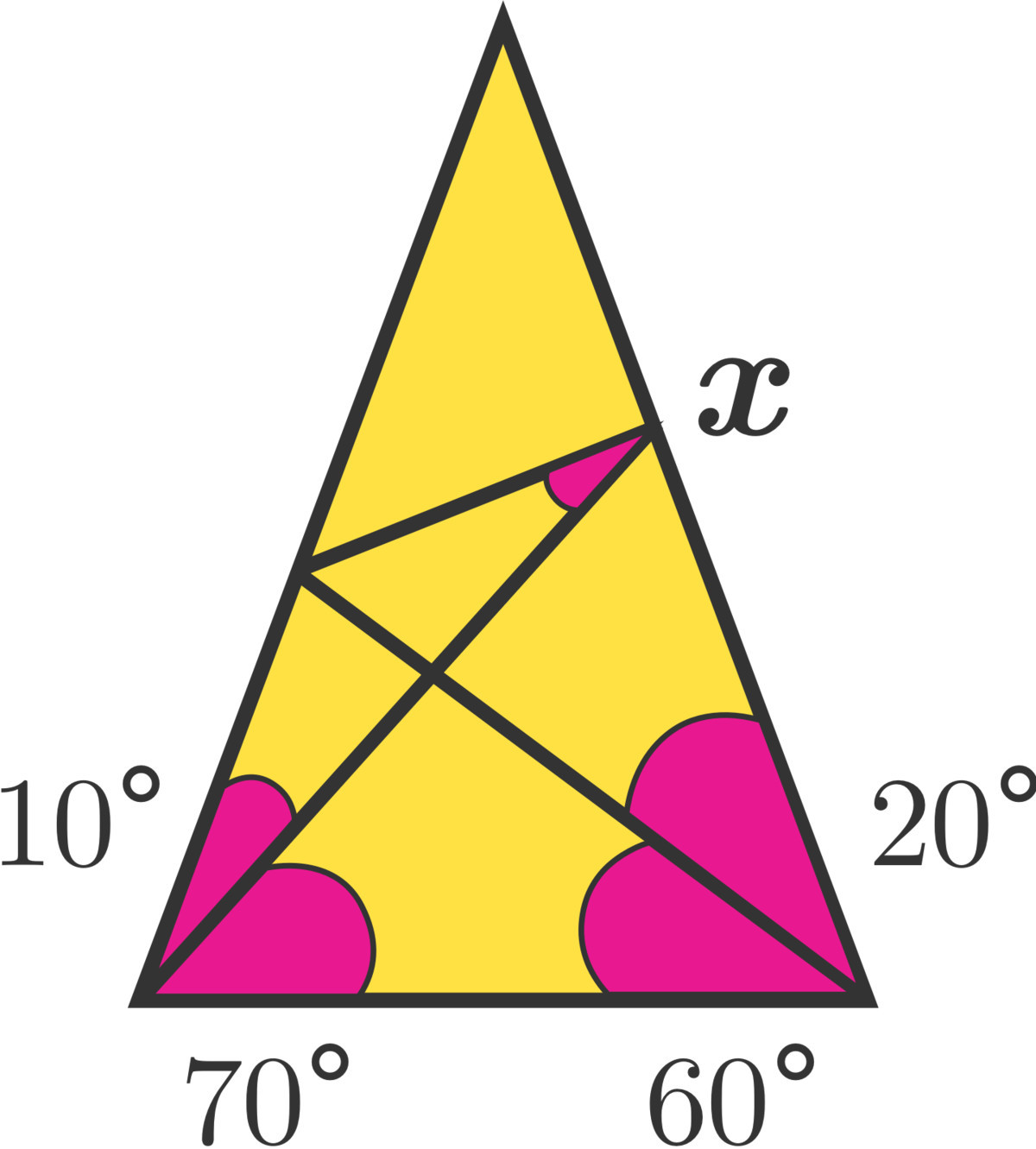
Draw in (red) lines A F , D F , C G at angles and between points as shown in graphic. Triangle D G F is equilateral, and all other integer angles as shown are easily found through angle chasing.
Because triangle A F C is isosceles, A F = C F . From this, we know that triangles A F E and C F G are congruent.
Therefore G F = E F , and since D F = G F , we know D F = E F , and conclude that triangle D F E is isosceles.
Therefore, ∠ D E F = 5 0 , and from this we have ∠ A E D = 2 0