Funny yet complicated!!!

Geometry Level 2

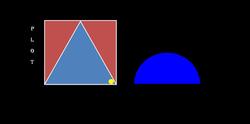The side of the square(red) is named plot.The side of the square is equal to that of the triangle's base.The base of the triangle is again equal to that of the semicircle.Find one of the angles of triangle marked yellow,if the area of the triangle is equal to that of the semi-circle. Note: The perpendicular to the base of the triangle cuts the base in half.

not enough information 57.5(degree) equal to that of an equilateral triangle 25% of 71.6(degree)

Shakil Md Resvy by Shakil Md Resvy , 22, Bangladesh

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Shakil Md Resvy
Oct 5, 2014

A/Q the side of the square is equal to the base of the triangle.Now,let take the base as x.Then the base of the semi-circle is also x.Again,consider the angle marked in yellow as y.Then, draw a line perpendicular to the base and the angle.This give us the height.Also,the base is halved.Now,we can use trigonometry.Since,the angle is y and and line below it is x/2.Therefore,the height is x/2 tan y. And the area is x^2/4 tan y.Again,the base of the semicircle is x.Since,it is also it's diameter,therefore,the radius is x/2.Hence the area is x^2/8 pi.A/Q,these two areas are equal.So,x^2/4 tan y =x^2/8 pi.Therefore,tan y=pi/2.Hence,y=57.5.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

THIS QUESTION IS FUNDAMENTALLY FLAWED.

As we all know; The Area of any Triangle is calculated using base and height. This Triangle as described has a constant base and a constant height (both defined as "plot"). Therefore

THE AREA OF THE TRIANGLE AS DESCRIBED REMAINS CONSTANT FOR ANY ANGLE BETWEEN 45 AND 90 DEGREES. (These are the possible range of values for the angle as described)

And at NO POINT will it ever be the same as the Area of the Semicircle as described.

Let the side of the square, aka "plot," be known as "x"

According to the description, base also equals x.

Area of a Triangle is (1/2)(base)(height), so the Area of our Triangle is (1/2)(x)(x), or (1/2)(x^2)

Area of a Semicircle is (1/2) radius squared, so the Area of our Semicircle is (1/8)(Pi)(x^2)

Setting the Area of the Triangle equal to the Area of the Semicircle, and attempting to solve for "x," the variable falls out of the equation, leaving an erroneous equation.

This is because the Area of the Triangle as described by the question simply does not equal the Area of the Semicircle as described by the question.

Kevin Hokr - 4 years, 3 months ago

@Shakil Md Resvy : The error in your reasoning is the assumption that the line "perpendicular to the base and the angle," happens to be at the midpoint of the base.

Kevin Hokr - 4 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...