Futoshiki

Logic Level 1

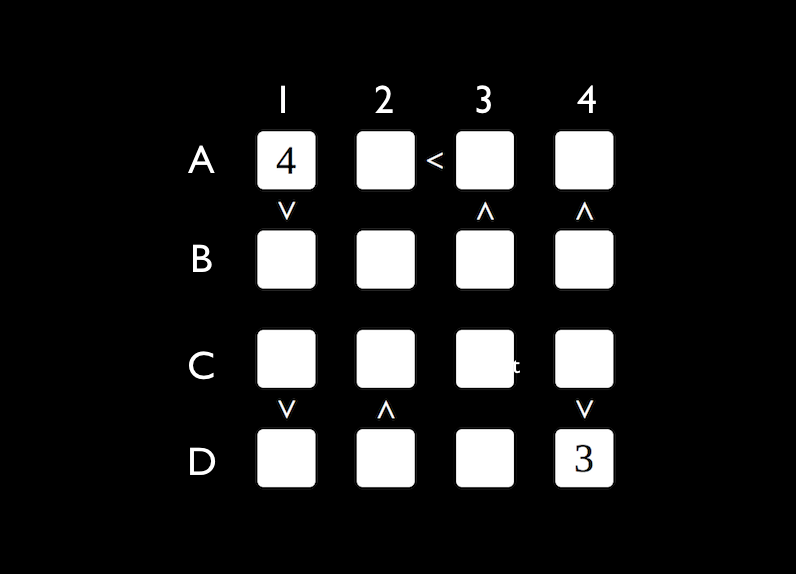
What are the digits of row A? (left to right)

Enter as a 4 digit number.


The answer is 4231.

Pigeon Mathlete by Pigeon Mathlete , 15, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Pigeon Mathlete
Nov 22, 2018

3 Helpful 0 Interesting 0 Brilliant 0 Confused

You can find row A, but there are 2 possible solutions to this puzzle as a whole. Isn't the rule that Futoshiki should only have 1 possible solution? Not that we wouldn't be able to answer it but still.

(What I am saying is, some of the digits can be switched. I reached solving where I only had left: B1 (digits 1/3), B2 (digits 1/3), C1 (digits 2/3), C2 (digits 1/3), C3 (digits 1/2), D1 (digits 1/2) and D3 (digits 1/2). You could easily switch B1 and B2 - 3 and 1 respectively, then row C - C1, C2 and C3 could be 2, 3 and 1 respectively, and finally D1 and D3 - 1 and 2 respectively.

Those who reached this point would understand easily what I'm trying to say, my goal is not to explain how I got here but just offer that there could be 2 possible solutions to your puzzle, which does not respect the rule of Futoshiki of only having 1 possible solution. Great doing though, your puzzle does work, maybe just add one more inequality sign or something, that's all)

Desanka Dimitrova - 11 months, 1 week ago
Kenny O.
Nov 23, 2018

Be cause of the arrow, we know that C4 must be 4. This means that B4 is 2 and A4 is 1 as B4>A4. As A3>A2 and 1 and 4 are used in the role, A3 must be 3 and A2 must be 2.
As the question only asks for row A, the answer is 4231

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Helpful, but still need to put a tad bit more heart into it.

Kiehl Y�igo Dela Fuente - 1 year ago

Psst. Excuse me Ken Kai, brilliant for brilliant? I put so much work into my explanation and not a single brilliant nor interesting nor helpful. Please.

Kiehl Y�igo Dela Fuente - 1 year ago

thank yoooooouuuu

Kiehl Y�igo Dela Fuente - 10 months, 3 weeks ago

Let's solve this in order and to do that, we will determine where 3 will be in row A. For starters, we know for sure it isn't in A-4 because of the 3 in D-4 which is against the rules because the same number can't be in the same column or row. We also know it can't be in A-2 because the inequality says that the number in A-3 is greater than 3, and the only thing that is greater than 3 is 4 but that is impossible because of the 4 in A-1. So through the process of elimination, the only place for 3 to be in row A is A-3. That's one step closer to completing row A. Also, the inequality says that A-3, AKA 3 is greater than A-2 which could be 1 or 2 since it is the only numbers missing. We don't know without absolute certainty where 1 and 2 is, but bare with me for a few more minutes. Since the inequality says that B-3 is greater than 3, B-3 is 4 since it is the only number greater than 3. And, since the inequality says that C-4 is greater than D-4, AKA 3, C-4 is you guessed it, 4. That's another step closer to your goal, 4 3 ! And may I remind you that in column 4, the only missing numbers are 1 and 2; and may I remind you again that the inequality says that B-4 is greater that A-4 which is on column 4. And the only numbers we can use on column 4 is 1 and 2. So column 4 from top to bottom is 1243 since 2 is greater than 1! Which means that A-4 is 1. Another step closer, 4_31! So the only number missing in row A, our goal is 2 which has one spot for it, A-2. Congrats! And to know for sure you completed row A correctly, you can double check that the inequality if they are true and you can check that if it has a same number in the same row and/or column. If somehow you double check and it appears to have a false inequality and/or a same number in a same row or column, why not start from the beginning and make sure you do everything right. You completed row A, your goal! Please give this a brilliant and no confused and also please leave a comment down below and I will reply if it is a question because I put a lot of work into this things. Thanks for reading!

0 Helpful 0 Interesting 1 Brilliant 0 Confused

Also, I'll be checking in daily for comments and if this looks so long that you don't want to read it, please bear with it and I vow this is going to be super helpful.

Kiehl Y�igo Dela Fuente - 1 year ago

Thank you for the intricate and "brilliant" solution!

Pigeon Mathlete - 1 year ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...